
【题目】
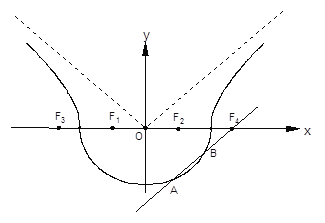
如图,曲线![]() 由曲线
由曲线![]() 和曲线
和曲线![]() 组成,其中点
组成,其中点![]() 为曲线
为曲线![]() 所在圆锥曲线的焦点,点
所在圆锥曲线的焦点,点![]() 为曲线
为曲线![]() 所在圆锥曲线的焦点;
所在圆锥曲线的焦点;
(1)若![]() ,求曲线
,求曲线![]() 的方程;
的方程;
(2)对于(1)中的曲线![]() ,若过点
,若过点![]() 作直线
作直线![]() 平行于曲线
平行于曲线![]() 的渐近线,交曲线
的渐近线,交曲线![]() 于点A、B,求三角形
于点A、B,求三角形![]() 的面积;
的面积;
(3)如图,若直线![]() (不一定过
(不一定过![]() )平行于曲线
)平行于曲线![]() 的渐近线,交曲线
的渐近线,交曲线![]() 于点A、B,求证:弦AB的中点M必在曲线
于点A、B,求证:弦AB的中点M必在曲线![]() 的另一条渐近线上.
的另一条渐近线上.
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在极坐标系中,O为极点,点![]() 在曲线
在曲线![]() 上,直线l过点
上,直线l过点![]() 且与
且与![]() 垂直,垂足为P.
垂直,垂足为P.
(1)当![]() 时,求
时,求![]() 及l的极坐标方程;
及l的极坐标方程;
(2)当M在C上运动且P在线段OM上时,求P点轨迹的极坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市一中学高三年级统计学生的最近20次数学周测成绩(满分150分),现有甲乙两位同学的20次成绩如茎叶图所示:
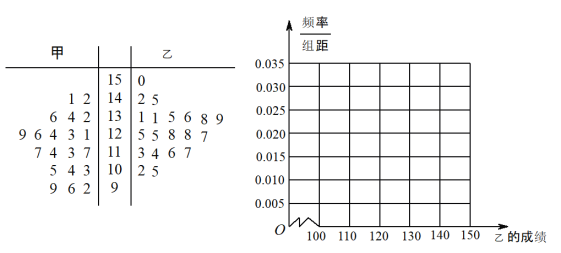
(1)根据茎叶图求甲乙两位同学成绩的中位数,并据此判断甲乙两位同学的成绩谁更好?
(2)将同学乙的成绩的频率分布直方图补充完整;
(3)现从甲乙两位同学的不低于140分的成绩中任意选出2个成绩,设选出的2个成绩中含甲的成绩的个数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
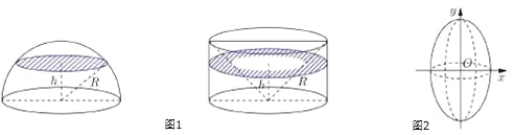
【题目】(数学文卷·2017届重庆十一中高三12月月考第16题) 现介绍祖暅原理求球体体积公式的做法:可构造一个底面半径和高都与球半径相等的圆柱,然后在圆柱内挖去一个以圆柱下底面圆心为顶点,圆柱上底面为底面的圆锥,用这样一个几何体与半球应用祖暅原理(图1),即可求得球的体积公式.请研究和理解球的体积公式求法的基础上,解答以下问题:已知椭圆的标准方程为![]() ,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
,将此椭圆绕y轴旋转一周后,得一橄榄状的几何体(图2),其体积等于______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“五行”是中国古代哲学的一种系统观,广泛用于中医、堪舆、命理、相术和占卜等方面.古人把宇宙万物划分为五种性质的事物,也即分成木、火、土、金、水五大类,并称它们为“五行”.中国古代哲学家用五行理论来说明世界万物的形成及其相互关系,创造了五行相生相克理论.相生,是指两类五行属性不同的事物之间存在相互帮助,相互促进的关系,具体是:木生火,火生土,土生金,金生水,水生木.相克,是指两类五行属性不同的事物之间是相互克制的关系,具体是:木克土,土克水,水克火、火克金、金克木.现从分别标有木,火,土,金,水的![]() 根竹签中随机抽取
根竹签中随机抽取![]() 根,则所抽取的
根,则所抽取的![]() 根竹签上的五行属性相克的概率为___________.
根竹签上的五行属性相克的概率为___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]()
![]() ,有下列四个命题:①
,有下列四个命题:①![]() 的值域是
的值域是![]() ;②
;②![]() 是奇函数;③
是奇函数;③![]() 在
在![]() 上单调递增;④方程
上单调递增;④方程![]() 总有四个不同的解;其中正确的是( )
总有四个不同的解;其中正确的是( )
A.①②B.②③C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知圆![]() ,圆
,圆![]() ,动圆
,动圆![]() 与圆
与圆![]() 外切并且与圆
外切并且与圆![]() 内切,圆心
内切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)![]() 是与圆
是与圆![]() ,圆
,圆![]() 都相切的一条直线,
都相切的一条直线,![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,当圆
两点,当圆![]() 的半径最长时,求
的半径最长时,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,
中,![]() 平面
平面![]() ,底面
,底面![]() 是直角梯形,其中
是直角梯形,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为棱
为棱![]() 上的点,且
上的点,且![]() .
.
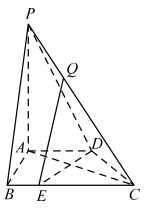
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值;
的余弦值;
(3)设![]() 为棱
为棱![]() 上的点(不与
上的点(不与![]() ,
,![]() 重合),且直线
重合),且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中,![]() ,前
,前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)证明:数列![]() 是等差数列,并写出其通项公式;
是等差数列,并写出其通项公式;
(3)设![]() (
(![]() ),试问是否存在正整数
),试问是否存在正整数![]() ,
,![]() (其中
(其中![]() ,使得
,使得![]() ,
,![]() ,
,![]() 成等比数列?若存在,求出所有满足条件的数对
成等比数列?若存在,求出所有满足条件的数对![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com