
【题目】已知函数f(x)=lnx﹣x2+ax,g(x)=ex﹣e,其中a>0.
(1)若a=1,证明:f(x)≤0;
(2)用max{m,n}表示m和n中的较大值,设函数h(x)=max{f(x),g(x)},讨论函数h(x)在(0,+∞)上的零点的个数.
【答案】(1)证明见解析;(2)当0<a≤1时,h(x)在(0,+∞)上有唯一的零点;当a>1时,h(x)在(0,+∞)上也有1个零点
【解析】
(1)对f(x)求导,然后求出f'(x)的零点,再判断f(x)的单调性,然后求出f(x)的最大值,进而证明f(x)≤0成立;
(2)由条件知h(x)在区间(1,+∞)上不可能有零点,然后根据条件考虑在区间(0,1)上和x=1处时h(x)的零点情况即可.
解:(1)![]() (x>0),
(x>0),
令f'(x)=0,则x=1或![]() (舍),
(舍),
∴当x∈(0,1)时,![]() >0,f(x)单调递增,
>0,f(x)单调递增,
当x∈(1,+∞)时,![]() <0,f(x)单调递减,
<0,f(x)单调递减,
∴f(x)≤f(x)max=f(1)=0.
(2)![]() 是
是![]() 上的增函数,
上的增函数,![]() ,
,
在区间(1,+∞)上,g(x)>0,∴h(x)=max{f(x),g(x)}≥g(x)>0,
∴h(x)在区间(1,+∞)上不可能有零点.
下面只考虑区间(0,1)上和x=1处的情况.
由题意f(x)的定义域为(0,+∞),![]() .
.
令![]() =0可得
=0可得![]() (负值舍去).
(负值舍去).
在(0,x0)上![]() >0,f(x)为增函数,在(x0,+∞)上
>0,f(x)为增函数,在(x0,+∞)上![]() <0,f(x)为减函数,
<0,f(x)为减函数,
∴f(x)max=f(x0).
①当a=1时,x0=1,∴f(x)max=f(1)=0.
∵在区间(0,1)上,g(x)<0,且g(1)=0,
∴此时h(x)存在唯一的零点x=1.
②当0<a<1时,![]() .
.
∵![]() ,∴
,∴![]() .
.
∴ ,
,
于是f(x)<0恒成立,结合函数g(x)的性质,
可知此时h(x)存在唯一的零点x=1.
③当a>1时,![]() ,∴f(x)在(0,1)上递增.
,∴f(x)在(0,1)上递增.
又∵f(1)=a﹣1>0,![]() ,
,
∴f(x)在区间(0,1)上存在唯一的零点x=x1.
结合函数g(x)的性质,可知x=x1是h(x)唯一的零点.
综上,当0<a≤1时,h(x)在(0,+∞)上有唯一的零点x=1;
当a>1时,h(x)在(0,+∞)上也有1个零点.


科目:高中数学 来源: 题型:
【题目】《中国诗词大会》(第三季)亮点颇多,在“人生自有诗意”的主题下,十场比赛每场都有一首特别设计的开场诗词在声光舞美的配合下,百人团齐声朗诵,别有韵味.若《沁园春·长沙》、《蜀道难》、《敕勒歌》、《游子吟》、《关山月》、《清平乐·六盘山》排在后六场,且《蜀道难》排在《游子吟》的前面,《沁园春·长沙》与《清平乐·六盘山》不相邻且均不排在最后,则后六场的排法有__________种.(用数字作答)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 点为圆
点为圆![]() 上的动点,点
上的动点,点![]() 在
在![]() 轴上的投影为
轴上的投影为![]() ,动点
,动点![]() 满足
满足![]() ,动点
,动点![]() 的轨迹为
的轨迹为![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)设![]() 的左顶点为
的左顶点为![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 交于两点
交于两点![]() ,
,![]() (
(![]() ,
,![]() 不是左右顶点),且满足
不是左右顶点),且满足![]() ,求证:直线
,求证:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,椭圆
上,椭圆![]() 的离心率是
的离心率是![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 为椭圆长轴的左端点,
为椭圆长轴的左端点,![]() 为椭圆上异于椭圆
为椭圆上异于椭圆![]() 长轴端点的两点,记直线
长轴端点的两点,记直线![]() 斜率分别为
斜率分别为![]() ,若
,若![]() ,请判断直线
,请判断直线![]() 是否过定点?若过定点,求该定点坐标,若不过定点,请说明理由.
是否过定点?若过定点,求该定点坐标,若不过定点,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
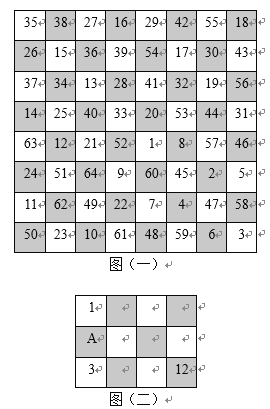
【题目】2018年国际象棋奥林匹克团体赛中国男队、女队同时夺冠.国际象棋中骑士的移动规则是沿着3×2格或2×3格的对角移动.在历史上,欧拉、泰勒、哈密尔顿等数学家研究了“骑士巡游”问题:在![]() 格的黑白相间的国际象棋棋盘上移动骑士,是否可以让骑士从某方格内出发不重复地走遍棋盘上的每一格?
格的黑白相间的国际象棋棋盘上移动骑士,是否可以让骑士从某方格内出发不重复地走遍棋盘上的每一格?
图(一)给出了骑士的一种走法,它从图上标1的方格内出发,依次经过标2,3,4,5,6,![]() ,到达标64的方格内,不重复地走遍棋盘上的每一格,又可从标64的方格内直接走回到标1的方格内.如果骑士的出发点在左下角标50的方格内,按照上述走法,_____(填“能”或“不能”)走回到标50的方格内.
,到达标64的方格内,不重复地走遍棋盘上的每一格,又可从标64的方格内直接走回到标1的方格内.如果骑士的出发点在左下角标50的方格内,按照上述走法,_____(填“能”或“不能”)走回到标50的方格内.
若骑士限制在图(二)中的3×4=12格内按规则移动,存在唯一一种给方格标数字的方式,使得骑士从左上角标1的方格内出发,依次不重复经过2,3,4,5,6,![]() ,到达右下角标12的方格内,分析图(二)中A处所标的数应为____.
,到达右下角标12的方格内,分析图(二)中A处所标的数应为____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市在节日期间进行有奖促销,凡在该超市购物满![]() 元的顾客,将获得一次摸奖机会,规则如下:一个袋子装有
元的顾客,将获得一次摸奖机会,规则如下:一个袋子装有![]() 只形状和大小均相同的玻璃球,其中两只是红色,三只是绿色,顾客从袋子中一次摸出两只球,若两只球都是红色,则奖励
只形状和大小均相同的玻璃球,其中两只是红色,三只是绿色,顾客从袋子中一次摸出两只球,若两只球都是红色,则奖励![]() 元;共两只球都是绿色,则奖励
元;共两只球都是绿色,则奖励![]() 元;若两只球颜色不同,则不奖励.
元;若两只球颜色不同,则不奖励.
(1)求一名顾客在一次摸奖活动中获得![]() 元的概率;
元的概率;
(2)记![]() 为两名顾客参与该摸奖活动获得的奖励总数额,求随机变量
为两名顾客参与该摸奖活动获得的奖励总数额,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com