把地球看作半径为R的球,设A、B两地纬度相同,都是α度,它们的经度相差β度(0<β≤180°),求A、B两地之间的球面距离.
分析:画出图形,由于A、B两地纬度相同,都是α度,先求纬圆半径,通过经度相差β度,解出AB距离,求出AB的球心角,然后求其球面距离.
解答:解:A、B两地之间的球面距离为过A、B所作之大圆的圆弧AB的长,
设其长为L,且设∠AOB=θ
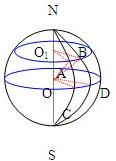
过A、B作平面O
1AB⊥NS(极轴),
此平面与球面交成圆O
1.
设其半径为r,由已知,∠AO
1B=β.
设C、D分别为赤道平面上与点A、B同经度之两点,
则由已知,∠AOC=∠BOD=α.
在过A、B的大圆上有
L=由此可知,只需求出θ即可.
在圆O
1中,线段AB=
2rsin,
又在过A、C的大圆中,因为∠OO
1A=90°,
∠OAO
1=α,所以r=Rcosα
代入上式,可得线段AB=
2Rcosαsin.
在△AOB中,线段AB=
2Rsin,
于是可得
2Rsin=
2Rcosαsin,
所以
θ=2arcsin(cosαsin).
由此可得A、B两地之间的球面距离为
L=arcsin(cosαsin).
此处之角度以度为单位.
点评:本题考查球面距离,经度不同纬度相同的一般问题,具体规律性,是中档题,好题.




 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案