
【题目】抛物线![]() 的焦点为F,过点F的直线交抛物线于A,B两点.
的焦点为F,过点F的直线交抛物线于A,B两点.
(1)若![]() ,求直线AB的斜率;
,求直线AB的斜率;
(2)设点M在线段AB上运动,原点O关于点M的对称点为C,求四边形OACB面积的最小值.
【答案】(1)![]() ;(2)面积最小值是4.
;(2)面积最小值是4.
【解析】
试题本题主要考查抛物线的标准方程及其几何性质、直线与圆锥曲线的位置关系、直线的斜率等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,依题意F(1,0),设直线AB的方程为![]() .将直线AB的方程与抛物线的方程联立,得
.将直线AB的方程与抛物线的方程联立,得![]() ,由此能够求出直线AB的斜率;第二问,由点C与原点O关于点M对称,得M是线段OC的中点,从而点O与点C到直线AB的距离相等,所以四边形OACB的面积等于
,由此能够求出直线AB的斜率;第二问,由点C与原点O关于点M对称,得M是线段OC的中点,从而点O与点C到直线AB的距离相等,所以四边形OACB的面积等于![]() ,由此能求出四边形OACB的面积的最小值.
,由此能求出四边形OACB的面积的最小值.
试题解析:(1)依题意知F(1,0),设直线AB的方程为![]() .将直线AB的方程与抛物线的方程联立,消去x得
.将直线AB的方程与抛物线的方程联立,消去x得![]() .设
.设![]() ,
,![]() ,所以
,所以![]() ,
,![]() .①因为
.①因为![]() ,所以
,所以![]() .②联立①和②,消去
.②联立①和②,消去![]() ,得
,得![]() .
.
所以直线AB的斜率是![]() .
.
(2)由点C与原点O关于点M对称,得M是线段OC的中点,从而点O与点C到直线AB的距离相等,所以四边形OACB的面积等于![]() .
.
因为![]() ,
,
所以当m=0时,四边形OACB的面积最小,最小值是4.



 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,已知asinB=bsin(A![]() ).
).
(1)求A;
(2)D是线段BC上的点,若AD=BD=2,CD=3,求△ADC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分形几何学是数学家伯努瓦·曼得尔布罗在20世纪70年代创立的一门新的数学学科,它的创立为解决传统科学众多领域的难题提供了全新的思路.按照如图甲所示的分形规律可得如图乙所示的一个树形图:记图乙中第![]() 行黑圈的个数为
行黑圈的个数为![]() ,则(1)
,则(1)![]() _______;(2)
_______;(2)![]() ______.
______.
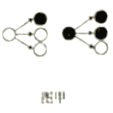
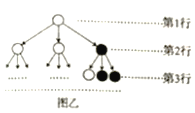
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《周髀算经》 是我国古代的天文学和数学著作。其中一个问题的大意为:一年有二十四个节气(如图),每个节气晷长损益相同(即物体在太阳的照射下影子长度的增加量和减少量相同).若冬至晷长一丈三尺五寸,夏至晷长一尺五寸(注:ー丈等于十尺,一尺等于十寸),则立冬节气的晷长为( )
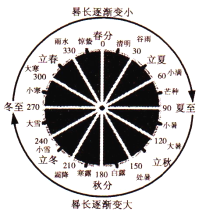
A. 九尺五寸 B. 一丈五寸 C. 一丈一尺五寸 D. 一丈六尺五寸
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市对所有高校学生进行普通话水平测试,发现成绩服从正态分布N(μ,σ2),下表用茎叶图列举出来抽样出的10名学生的成绩.
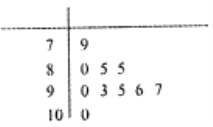
(1)计算这10名学生的成绩的均值和方差;
(2)给出正态分布的数据:P(μ﹣σ<X<μ+σ)=0.6826,P(μ﹣2σ<X<μ+2σ)=0.9544.
由(1)估计从全市随机抽取一名学生的成绩在(76,97)的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com