练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数
    （1）当时，求的极值
    （2）当时，求的单调区间
    （3）若对任意的，恒有成立，求实数的取值范围。

    （1）（2）见解析（3）

    解析

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    （本小题满分12分）
    已知函数 (R)．
    (1) 若，求函数的极值；
    （2）是否存在实数使得函数在区间上有两个零点，若存在，求出的取值范围；若不存在，说明理由。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （13分）已知函数f（x）=lnx，g（x）=（a≠0）
    （1）若b=2,且h（x）=f（x）-g（x）在定义域上不单调，求a的取值范围；
    （2）若a=1,b=-2设f（x）的图象C1与g（x）的图象C2交于点P、Q，过线段PQ的中点作x轴的垂线分别交C1，C2于点M、N，M、N的横坐标是m，求证：f＇（m）＜g＇（m）。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数（），．
    （Ⅰ）若，曲线在点处的切线与轴垂直，求的值；
    （Ⅱ）在（Ⅰ）的条件下，求证：；
    （Ⅲ）若，试探究函数与的图象在其公共点处是否存在公切线，若存在，研究值的个数；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    设，其中
    （Ⅰ）当时，求的极值点；
    （Ⅱ）若为R上的单调函数，求a的取值范围。

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    商场销售某种商品的经验表明，该商品每日的销售量(单位：千克)与销售价格(单位：元/千克)满足关系式，其中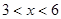，为常数，已知销售价格为5元/千克时，每日可售出该商品11千克．
    (1) 求的值；
    (2) 若商品的成品为3元/千克, 试确定销售价格的值,使商场每日销售该商品所获得的利润最大

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    已知函数f(x)＝2x－－aln(x＋1)，a∈R．
    （1）若a＝－4，求函数f(x)的单调区间；
    （2）求y＝f(x)的极值点（即函数取到极值时点的横坐标）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分13分）
    已知函数,，其中R．
    （1）当a=1时，判断的单调性；
    （2）若在其定义域内为增函数，求正实数的取值范围；
    （3）设函数,当时，若，，总有
    成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    （本小题满分14分）若函数，
    （1）当时，求函数的单调增区间；
    （2）函数是否存在极值.

    查看答案和解析>>

    同步练习册答案