练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知函数f（x）=cos（2x+φ），|φ|≤ ，若f（ ﹣x）=﹣f（x），则要得到y=sin2x的图象只需将y=f（x）的图象（ ）
    A.向左平移 个单位
    B.向右平移 个单位
    C.向左平移 个单位
    D.向右平移 个单位

    【答案】B
    【解析】解：函数f（x）=cos（2x+φ），|φ|≤ ，由 ，
    可得cos[2（ ﹣x）+φ]=﹣cos（2x+φ），
    整理得：cos（ φ）=﹣cos（2x+φ）=cos（π﹣（2x+φ]
    ∵φ|≤ ，
    ∴令 φ=π﹣（2x+φ）
    解得：φ=
    故函数f（x）=cos（2x ）=sin（2x + ）=sin（2x+ ）=sin2（x+ ）
    向右平移 个单位可得到sin2x．
    故选B．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设m，n（3≤m≤n）是正整数，数列Am：a1 ， a2 ， …，am ， 其中ai（1≤i≤m）是集合{1，2，3，…，n}中互不相同的元素．若数列Am满足：只要存在i，j（1≤i＜j≤m）使ai+aj≤n，总存在k（1≤k≤m）有ai+aj=ak ， 则称数列Am是“好数列”． （Ⅰ）当m=6，n=100时，
    （ⅰ）若数列A6：11，78，x，y，97，90是一个“好数列”，试写出x，y的值，并判断数列：11，78，90，x，97，y是否是一个“好数列”？
    （ⅱ）若数列A6：11，78，a，b，c，d是“好数列”，且a＜b＜c＜d，求a，b，c，d共有多少种不同的取值？
    （Ⅱ）若数列Am是“好数列”，且m是偶数，证明： ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若关于x的不等式ex﹣（a+1）x﹣b≥0（e为自然对数的底数）在R上恒成立，则（a+1）b的最大值为（ ）
    A.e+1
    B.e+
    C.
    D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=x﹣alnx（a∈R）
    （1）当a=2时，求曲线y=f（x）在点A（1，f（1））处的切线方程；
    （2）求函数f（x）的极值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知命题p：函数f（x）=lg（ax2﹣ax+1）的定义域是R；命题 在第一象限为增函数，若“p∧q”为假，“p∨q”为真，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=2sinωx，其中常数ω＞0．
    （Ⅰ）令ω=1，求函数 在 上的最大值；
    （Ⅱ）若函数 的周期为π，求函数g（x）的单调递增区间，并直接写出g（x）在 的零点个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知x，y∈[0，π]，则cos（x+y）+cosx+2cosy的最小值为 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知等差数列{an}的前n项和为Sn ， 且a1=10，S5≥S6 ， 下列四个命题中，假命题是（ ）
    A.公差d的最大值为﹣2
    B.S7＜0
    C.记Sn的最大值为K，K的最大值为30
    D.a2016＞a2017

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】四棱锥P﹣ABCD中，PD⊥面ABCD，底面ABCD是菱形，且PD=DA=2，∠CDA=60°，过点B作直线l∥PD，Q为直线l上一动点．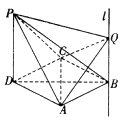
    （1）求证：QP⊥AC；
    （2）当二面角Q﹣AC﹣P的大小为120°时，求QB的长；
    （3）在（2）的条件下，求三棱锥Q﹣ACP的体积．

    查看答案和解析>>

    同步练习册答案