
【题目】已知椭圆E:![]() =1(a>b>0)过点A
=1(a>b>0)过点A![]() ,离心率为
,离心率为![]() ,点F1,F2分别为其左、右焦点.
,点F1,F2分别为其左、右焦点.
(1)求椭圆E的标准方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆E恒有两个交点P,Q,且![]() ?若存在,求出该圆的方程,并求|PQ|的最大值;若不存在,请说明理由.
?若存在,求出该圆的方程,并求|PQ|的最大值;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由椭圆的离心率为![]() 可得
可得![]() ,故椭圆的方程为
,故椭圆的方程为![]() ,再根据点A
,再根据点A![]() 在椭圆上得到
在椭圆上得到![]() ,于是可得方程为
,于是可得方程为![]() .(2)假设满足条件的圆存在,其方程为
.(2)假设满足条件的圆存在,其方程为![]() ,然后分直线PQ的斜率存在和不存在两种情况讨论可得存在满足题意得圆,其方程为
,然后分直线PQ的斜率存在和不存在两种情况讨论可得存在满足题意得圆,其方程为![]() ;最后根据弦长公式和二次函数的知识得到|PQ|max=
;最后根据弦长公式和二次函数的知识得到|PQ|max=![]() .
.
(1)由题意得e=![]() ,
,
所以![]() ,
,
故椭圆的方程为![]() ,
,
因为点A![]() 在椭圆上,
在椭圆上,
所以![]() ,
,
解得![]() ,
,
所以椭圆E方程为![]() .
.
(2)假设满足条件的圆存在,其方程为![]() .
.
①当直线PQ的斜率存在时,设直线方程为![]() ,
,
由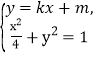 消去y整理得(1+4k2)x2+8mkx+4m2-4=0,
消去y整理得(1+4k2)x2+8mkx+4m2-4=0,
令P(x1,y1),Q(x2,y2),
则x1+x2=-![]() ,x1x2=
,x1x2=![]() .
.
∵![]() ,
,
∴x1x2+y1y2=0.
∴![]() +m2=0.
+m2=0.
∴5m2=4k2+4.
由直线PQ与圆相切,则r2=![]() .
.
所以存在圆满足题意,且圆的方程为![]() .
.
②当直线PQ的斜率不存在时,也适合![]() .
.
综上所述,存在圆心在原点的圆![]() 满足题意.
满足题意.
由弦长公式可得|PQ|=![]()
![]()
![]() .
.
又b2=![]() k2+
k2+![]() ,
,
代入上式可得|PQ|=![]() .
.
令4k2+1=t,即k2=![]() ,t≥1,
,t≥1,
则|PQ|=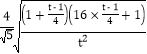 =
=![]() =
=![]() ,
,
当![]() 时,即k=±
时,即k=±![]() 时,|PQ|max=
时,|PQ|max=![]() .
.
当直线的斜率k不存在时,|PQ|=|y1-y2|=![]() ,
,
综上可得|PQ|max=![]() .
.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,O为AD的中点,射线OP从OA出发,绕着点O顺时针方向旋转至OD,在旋转的过程中,记∠AOP为x(x∈[0,π]),OP所经过正方形ABCD内的区域(阴影部分)的面积S=f(x),那么对于函数f(x)有以下三个结论:
①f( ![]() )=
)= ![]() ;
;
②任意x∈[0, ![]() ],都有f(
],都有f( ![]() ﹣x)+f(
﹣x)+f( ![]() +x)=4;
+x)=4;
③任意x1 , x2∈( ![]() ,π),且x1≠x2 , 都有
,π),且x1≠x2 , 都有 ![]() <0.
<0.
其中所有正确结论的序号是 . 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列说法:
①一支田径队有男女运动员98人,其中男运动员有56人.按男、女比例用分层抽样的方法,从全体运动员中抽出一个容量为28的样本,那么应抽取女运动员人数是12人;
②采用系统抽样法从某班按学号抽取5名同学参加活动,学号为5,27,38,49的同学均选中,则该班学生的人数为60人;
③废品率x%和每吨生铁成本y(元)之间的回归直线方程为 ![]() ,这表明废品率每增加1%,生铁成本大约增加258元;
,这表明废品率每增加1%,生铁成本大约增加258元;
④为了检验某种血清预防感冒的作用,把500名未使用血清和使用血清的人一年中的感冒记录作比较,提出假设H0:“这种血清不能起到预防作用”,利用2×2列联表计算得K2的观测值k≈3.918,经查对临界值表知P(K2≥3.841)≈0.05,由此,得出以下判断:在犯错误的概率不超过0.05的前提下认为“这种血清能起到预防的作用”.
正确的有( )
A.①④
B.②③
C.①③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某调查机构观察了某地100个新生婴儿的体重,并根据所得数据画出了样本的频率分布直方图如图,则新生婴儿的体重在[3.2,4.0)(kg)的有人.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx,g(x)=﹣x2+ax﹣3.
(1)求f(x)在[t,t+2](t>0)上的最小值;
(2)若存在x ![]() 使不等式2f(x)≥g(x)成立,求实数a的取值范围.
使不等式2f(x)≥g(x)成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学生社团对本校学生学习方法开展问卷调查的过程中发现,在回收上来的1000份有效问卷中,同学们背英语单词的时间安排有两种:白天背和晚上临睡前背。为研究背单词时间安排对记忆效果的影响,该社团以5%的比例对这1000名学生按时间安排进行分层抽样,并完成一项试验,试验方法是:使两组学生记忆40个无意义音节(如xiq,geh),均要求刚能全部记清就停止识记,并在8小时后进行记忆测验。不同的是,甲组同学识记结束后一直不睡觉,8小时后测验;乙组同学识记停止后立刻睡觉,8小时后叫醒测验。两组同学识记停止8小时后的准确回忆(保持)情况如图(区间含左端点不含右端点)。

(1)估计1000名被调查的学生中识记停止8小时后40个音节的保持率大于或等于60%的人数;
(2)从乙组准确回忆个数在![]() 范围内的学生中随机选3人,记:能准确回忆20个以上(含20)的人数为随机变量X,求X的分布列及数学期望;
范围内的学生中随机选3人,记:能准确回忆20个以上(含20)的人数为随机变量X,求X的分布列及数学期望;
(3)从本次试验的结果来看,上述两种时间安排方法中哪种方法背英语单词记忆效果更好?计算并说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com