
【题目】已知函数![]()
![]() 有两个不同的零点.
有两个不同的零点.
(1)求![]() 的取值范围;
的取值范围;
(2)设![]() ,
, ![]() 是
是![]() 的两个零点,证明:
的两个零点,证明: ![]() .
.
【答案】(1) ![]() (2)见解析
(2)见解析
【解析】试题分析:(1)求出![]() ,分四种情况讨论
,分四种情况讨论![]() 的范围,在定义域内,分别令
的范围,在定义域内,分别令![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 增区间,
增区间, ![]() 求得
求得![]() 的范围,可得函数
的范围,可得函数![]() 的减区间,根据单调性,结合函数草图可筛选出符合题意的
的减区间,根据单调性,结合函数草图可筛选出符合题意的![]() 的取值范围;(2)构造函数设
的取值范围;(2)构造函数设![]() ,
, ![]() ,可利用导数证明∴
,可利用导数证明∴![]() ,∴
,∴![]() ,
,
于是![]() ,即
,即![]() ,
, ![]() 在
在![]() 上单调递减,可得
上单调递减,可得![]() ,进而可得结果.
,进而可得结果.
试题解析:(1)【解法一】
函数![]() 的定义域为:
的定义域为: ![]() .
.
![]()
![]() ,
,
①当![]() 时,易得
时,易得![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
则![]() 至多只有一个零点,不符合题意,舍去.
至多只有一个零点,不符合题意,舍去.
②当![]() 时,令
时,令![]() 得:
得: ![]() ,则
,则
|
|
|
|
| + | 0 | - |
| 增 | 极大 | 减 |
∴![]()
![]() .
.
设![]() ,∵
,∵![]() ,则
,则![]() 在
在![]() 上单调递增.
上单调递增.
又∵![]() ,∴
,∴![]() 时,
时, ![]() ;
; ![]() 时,
时, ![]() .
.
因此:
(i)当![]() 时,
时, ![]() ,则
,则![]() 无零点,
无零点,
不符合题意,舍去.
(ii)当![]() 时,
时, ![]() ,
,
∵![]()
![]() ,∴
,∴![]() 在区间
在区间![]() 上有一个零点,
上有一个零点,
∵![]()
![]()
![]() ,
,
设![]() ,
, ![]() ,∵
,∵![]() ,
,
∴![]() 在
在![]() 上单调递减,则
上单调递减,则![]() ,
,
∴![]() ,
,
∴![]() 在区间
在区间![]() 上有一个零点,那么,
上有一个零点,那么, ![]() 恰有两个零点.
恰有两个零点.
综上所述,当![]() 有两个不同零点时,
有两个不同零点时, ![]() 的取值范围是
的取值范围是![]() .
.
(1)【解法二】
函数的定义域为: ![]() .
. ![]()
![]() ,
,
①当![]() 时,易得
时,易得![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
则![]() 至多只有一个零点,不符合题意,舍去.
至多只有一个零点,不符合题意,舍去.
②当![]() 时,令
时,令![]() 得:
得: ![]() ,则
,则
|
|
|
|
| + | 0 | - |
| 增 | 极大 | 减 |
∴![]()
![]() .
.
∴要使函数![]() 有两个零点,则必有
有两个零点,则必有![]() ,即
,即![]() ,
,
设![]() ,∵
,∵![]() ,则
,则![]() 在
在![]() 上单调递增,
上单调递增,
又∵![]() ,∴
,∴![]() ;
;
当![]() 时:
时:
∵![]()
![]() ,
,
∴![]() 在区间
在区间![]() 上有一个零点;
上有一个零点;
设![]() ,
,
∵![]() ,∴
,∴![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴![]() ,∴
,∴![]() ,
,
∴![]()
![]()
![]() ,
,
则![]() ,∴
,∴![]() 在区间
在区间![]() 上有一个零点,
上有一个零点,
那么,此时![]() 恰有两个零点.
恰有两个零点.
综上所述,当![]() 有两个不同零点时,
有两个不同零点时, ![]() 的取值范围是
的取值范围是![]() .
.
(2)【证法一】
由(1)可知,∵![]() 有两个不同零点,∴
有两个不同零点,∴![]() ,且当
,且当![]() 时,
时, ![]() 是增函数;
是增函数;
当![]() 时,
时, ![]() 是减函数;
是减函数;
不妨设: ![]() ,则:
,则: ![]() ;
;
设![]() ,
, ![]() ,
,
则: ![]()
![]()
![]()
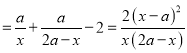 .
.
当![]() 时,
时, ![]() ,∴
,∴![]() 单调递增,又∵
单调递增,又∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
∵![]() ,
, ![]() ,
, ![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,∴
,∴![]() .
.
(2)【证法二】
由(1)可知,∵![]() 有两个不同零点,∴
有两个不同零点,∴![]() ,且当
,且当![]() 时,
时, ![]() 是增函数;
是增函数;
当![]() 时,
时, ![]() 是减函数;
是减函数;
不妨设: ![]() ,则:
,则: ![]() ;
;
设![]() ,
, ![]() ,
,
则![]()
![]()
![]()
![]() .
.
当![]() 时,
时, ![]() ,∴
,∴![]() 单调递增,
单调递增,
又∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,
,
∴![]()
![]()
![]() ,
,
∵![]() ,
, ![]() ,
, ![]() 在
在![]() 上单调递减,
上单调递减,
∴![]() ,∴
,∴![]() .
.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:
【题目】设全集U=R,集合A={x|-1≤x<3},B={x|2x-4≥x-2}.
(1)求U(A∩B);
(2)若集合C={x|2x+a>0},满足B∪C=C,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取![]() 次.记录如下:
次.记录如下:
甲: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
乙: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
(![]() )用茎叶图表示这两组数据.
)用茎叶图表示这两组数据.
(![]() )现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为派哪位学生参加合适?请说明理由.
)现要从中选派一人参加数学竞赛,从统计学的角度考虑,你认为派哪位学生参加合适?请说明理由.
(![]() )若将频率视为概率,对甲同学在今后的三次数学竞赛成绩进行预测,记这
)若将频率视为概率,对甲同学在今后的三次数学竞赛成绩进行预测,记这![]() 次成绩中高于
次成绩中高于![]() 分的次数为
分的次数为![]() ,求
,求![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
:![]() ,圆
,圆![]() :
:![]() ,动圆
,动圆![]() 与圆
与圆![]() 外切并且与圆
外切并且与圆![]() 内切,圆心
内切,圆心![]() 轨迹为曲线
轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)若![]() 是曲线
是曲线![]() 上关于
上关于![]() 轴对称的两点,点
轴对称的两点,点![]() ,直线
,直线![]() 交曲线
交曲线![]()
于另一点![]() ,求证:直线
,求证:直线![]() 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小李在做一份调查问卷,共有4道题,其中有两种题型,一种是选择题,共2道,另一种是填空题,共2道.
(1)小李从中任选2道题解答,每一次选1题(不放回),求所选的题不是同一种题型的概率;
(2)小李从中任选2道题解答,每一次选1题(有放回),求所选的题不是同一种题型的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若数列{an}是公差为2的等差数列,数列{bn}满足b1=1,b2=2,且anbn+bn=nbn+1.
(1)求数列{an},{bn}的通项公式;
(2)设数列{cn}满足![]() ,数列{cn}的前n项和为Tn,若不等式(-1)nλ<Tn+
,数列{cn}的前n项和为Tn,若不等式(-1)nλ<Tn+![]() 对一切n∈N*恒成立,求实数λ的取值范围.
对一切n∈N*恒成立,求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】正△ABC的边长为2, CD是AB边上的高,E、F分别是AC和BC的中点(如图(1)).现将△ABC沿CD翻成直二面角A-DC-B(如图(2)).在图(2)中:
(1)求证:AB∥平面DEF;
(2)在线段BC上是否存在一点P,使AP⊥DE?证明你的结论;
(3)求二面角E-DF-C的余弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校进行文科、理科数学成绩对比,某次考试后,各随机抽取100名同学的数学考试成绩进行统计,其频率分布表如下.

(Ⅰ)根据数学成绩的频率分布表,求理科数学成绩的中位数的估计值;(精确到0.01)
(Ⅱ)请填写下面的列联表,并根据列联表判断是否有90%的把握认为数学成绩与文理科有关:

参考公式与临界值表: 
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com