
【题目】已知函数![]() ,其中
,其中![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)讨论函数![]() 零点的个数;
零点的个数;
(3)若![]() 存在两个不同的零点
存在两个不同的零点![]() ,求证:
,求证:![]() .
.
【答案】(1)增区间为![]() ,
,![]() ,减区间为
,减区间为![]() (2)见解析 (3)证明见解析
(2)见解析 (3)证明见解析
【解析】
(1)先求出![]() 的定义域,求得导函数
的定义域,求得导函数![]() ,令
,令![]() 可解得
可解得![]() 或
或![]() ,分类讨论判断
,分类讨论判断![]() 或
或![]() ,进而解得单调区间;
,进而解得单调区间;
(2)整理函数为![]() ,则令
,则令![]() ,当
,当![]() 时,
时,![]() ,则分别讨论
,则分别讨论![]() 和
和![]() 两种情况,利用零点存在性定理判断零点个数;
两种情况,利用零点存在性定理判断零点个数;
(3)由(2)可知![]() ,构造函数
,构造函数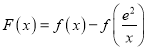 ,利用导数可得
,利用导数可得![]() 在
在![]() 单调递增,则
单调递增,则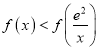 ,整理即可得证
,整理即可得证
解:(1)函数![]() 的定义域为
的定义域为![]() ,
,
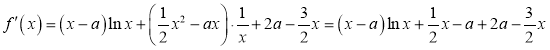
![]()
令![]() ,得
,得![]() 或
或![]() ,
,
因为![]() ,当
,当![]() 或
或![]() 时,
时,![]() ,
,![]() 单调递增;
单调递增;
当![]() 时,
时,![]() ,
,![]() 单调递减,
单调递减,
所以![]() 的增区间为
的增区间为![]() ,
,![]() ;减区间为
;减区间为![]()
(2)取![]() ,则当
,则当![]() 时,
时,![]() ,
,![]() ,
,![]()
所以![]() ;
;
又因为![]() ,由(1)可知
,由(1)可知![]() 在
在![]() 上单调递增,因此,当
上单调递增,因此,当![]() ,
,![]() 恒成立,即
恒成立,即![]() 在
在![]() 上无零点.;
上无零点.;
下面讨论![]() 的情况:
的情况:
①当![]() 时,因为
时,因为![]() 在
在![]() 单调递减,
单调递减,![]() 单调递增,且
单调递增,且![]() ,
,![]() ,
,![]() ,
,
根据零点存在定理,![]() 有两个不同的零点;
有两个不同的零点;
②当![]() 时,由
时,由![]() 在
在![]() 单调递减,
单调递减,![]() 单调递增,且
单调递增,且![]() ,
,
此时![]() 有唯一零点
有唯一零点![]() ;
;
③若![]() ,由
,由![]() 在
在![]() 单调递减,
单调递减,![]() 单调递增,
单调递增,![]() ,
,
此时![]() 无零点;
无零点;
综上,若![]() ,
,![]() 有两个不同的零点;若
有两个不同的零点;若![]() ,
,![]() 有唯一零点
有唯一零点![]() ;若
;若![]() ,
,![]() 无零点
无零点
(3)证明:由(2)知,![]() ,且
,且![]() ,
,
构造函数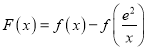 ,
,![]() ,
,
则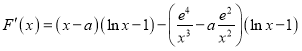
![]() ,
,
令![]() ,
,![]() ,
,
因为当![]() 时,
时,![]() ,
,![]() ,
,
所以![]()
又![]() ,所以
,所以![]() 恒成立,即
恒成立,即![]() 在
在![]() 单调递增,
单调递增,
于是当![]() 时,
时,![]() ,即
,即 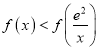 ,
,
因为![]() ,所
,所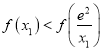 ,
,
又![]() ,所以
,所以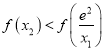 ,
,
因为![]() ,
,![]() ,且
,且![]() 在
在![]() 单调递增,
单调递增,
所以由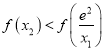 ,可得
,可得![]() ,即
,即![]()


科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,将曲线
中,将曲线![]() (
(![]() 为参数)上任意一点
为参数)上任意一点![]() 经过伸缩变换
经过伸缩变换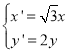 后得到曲线
后得到曲线![]() 的图形.以坐标原点
的图形.以坐标原点![]() 为极点,x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,已知直线
为极点,x轴的非负半轴为极轴,取相同的单位长度建立极坐标系,已知直线![]() .
.
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)点P为曲线![]() 上的任意一点,求点P到直线
上的任意一点,求点P到直线![]() 的距离的最大值及取得最大值时点P的坐标.
的距离的最大值及取得最大值时点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (a>b>0)长轴的两顶点为A、B,左右焦点分别为F1、F2,焦距为2c且a=2c,过F1且垂直于x轴的直线被椭圆C截得的线段长为3.
(a>b>0)长轴的两顶点为A、B,左右焦点分别为F1、F2,焦距为2c且a=2c,过F1且垂直于x轴的直线被椭圆C截得的线段长为3.
(1)求椭圆C的方程;
(2)在双曲线![]() 上取点Q(异于顶点),直线OQ与椭圆C交于点P,若直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4,试证明:k1+k2+k3+k4为定值;
上取点Q(异于顶点),直线OQ与椭圆C交于点P,若直线AP、BP、AQ、BQ的斜率分别为k1、k2、k3、k4,试证明:k1+k2+k3+k4为定值;
(3)在椭圆C外的抛物线K:y2=4x上取一点E,若EF1、EF2的斜率分别为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司进行共享单车的投放与损耗统计,到去年![]() 年底单车的市场保有量(已投入市场且能正常使用的单车数量)为
年底单车的市场保有量(已投入市场且能正常使用的单车数量)为![]() 辆,预计今后每年新增单车1000辆,随着单车的频繁使用,估计每年将有200辆车的损耗,并且今后若干年内,年平均损耗在上一年损耗基础上增加
辆,预计今后每年新增单车1000辆,随着单车的频繁使用,估计每年将有200辆车的损耗,并且今后若干年内,年平均损耗在上一年损耗基础上增加![]() %.
%.
(1)预计![]() 年底单车的市场保有量是多少?
年底单车的市场保有量是多少?
(2)到哪一年底,市场的单车保有量达到最多?该年的单车保有量是多少辆(最后结果精确到整数)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为满足人们的阅读需求,图书馆设立了无人值守的自助阅读区,提倡人们在阅读后将图书分类放回相应区域.现随机抽取了某阅读区500本图书的分类归还情况,数据统计如下(单位:本).
文学类专栏 | 科普类专栏 | 其他类专栏 | |
文学类图书 | 100 | 40 | 10 |
科普类图书 | 30 | 200 | 30 |
其他图书 | 20 | 10 | 60 |
(1)根据统计数据估计文学类图书分类正确的概率;
(2)根据统计数据估计图书分类错误的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com