
【题目】对于定义在![]() 上的函数
上的函数![]() ,若存在正常数
,若存在正常数![]() 、
、![]() ,使得
,使得![]() 对一切
对一切![]() 均成立,则称
均成立,则称![]() 是“控制增长函数”.在以下四个函数中:①
是“控制增长函数”.在以下四个函数中:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .是“控制增长函数”的有( )个
.是“控制增长函数”的有( )个
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数,
为奇函数,![]() ,其中
,其中![]() .
.
(1)若函数![]() 的图像过点
的图像过点![]() ,求实数
,求实数![]() 和
和![]() 的值;
的值;
(2)若![]() ,试判断函数
,试判断函数![]() 在
在![]() 上的单调性并证明;
上的单调性并证明;
(3)设函数 ,若对每一个不小于3的实数
,若对每一个不小于3的实数![]() ,都恰有一个小于3的实数
,都恰有一个小于3的实数![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() :
:![]() 经过点
经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 是椭圆
是椭圆![]() 上的任意一点,射线
上的任意一点,射线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点,直线
有且只有一个公共点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两个相异点,证明:
两个相异点,证明:![]() 面积为定值.
面积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 满足:对于任意正数
满足:对于任意正数![]() ,
,![]() ,都有
,都有![]() ,
,![]() ,且
,且![]() ,则称函数
,则称函数![]() 为“速增函数”.
为“速增函数”.
(1)试判断函数![]() 与
与![]() 是否是“速增函数”;
是否是“速增函数”;
(2)若函数![]() 为“速增函数”,求
为“速增函数”,求![]() 的取值范围;
的取值范围;
(3)若函数![]() 为“速增函数”,且
为“速增函数”,且![]() ,求证:对任意
,求证:对任意![]() ,都有
,都有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,点
是菱形,点![]() 在线段
在线段![]() 上,
上,![]() ,
,![]() 是线段
是线段![]() 的中点,且三棱锥
的中点,且三棱锥![]() 的体积是四棱锥
的体积是四棱锥![]() 体积的
体积的![]() .
.
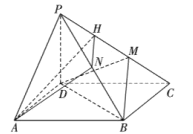
(1)若![]() 是
是![]() 的中点,证明:平面
的中点,证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 平面
平面![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】程大位是明代著名数学家,他的《新编直指算法统宗》是中国历史上一部影响巨大的著作.卷八中第33问:“今有三角果一垛,底阔每面七个.问该若干?”如图是解决该问题的程序框图.执行该程序框图,求得该垛果子的总数S为( )
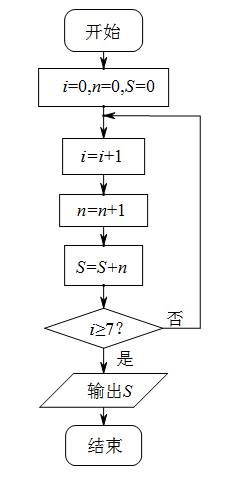
A.28B.56C.84D.120
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数![]() 的定义域
的定义域![]() 恰是不等式
恰是不等式![]() 的解集,其值域为
的解集,其值域为![]() ,函数
,函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() .
.
(1)求![]() 定义域
定义域![]() 和值域
和值域![]() ;
;
(2)试用单调性的定义法解决问题:若存在实数![]() ,使得函数
,使得函数![]() 在
在![]() 上单调递减,
上单调递减,![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围并用
的取值范围并用![]() 表示
表示![]() ;
;
(3)是否存在实数![]() ,使
,使![]() 成立?若存在,求实数
成立?若存在,求实数![]() 的取值范围,若不存在,说明理由.
的取值范围,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com