
【题目】2017年被称为“新高考元年”,随着上海、浙江两地顺利实施“语数外+3”新高考方案,新一轮的高考改革还将继续在全国推进。辽宁地区也将于2020年开启新高考模式,今年秋季入学 的高一新生将面临从物理、化学、生物、政治、历史、地理等6科中任选三科(共20种选法)作为 自己将来高考“语数外+3 ”新高考方案中的“3”。某地区为了顺利迎接新高考改革,在某学校理科班的200名学生中进行了“学生模拟选科数据”调查,每个学生只能从表格中的20种课程 组合选择一种学习。模拟选课数据统计如下表:
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
组合学科 | 物化生 | 物化政 | 物化历 | 物化地 | 物生政 | 物生历 | 物生地 |
人数 | 20人 | 5人 | 10人 | 10人 | 10人 | 15人 | 10人 |
序号 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
组合学科 | 物政历 | 物政地 | 物历地 | 化生政 | 化生历 | 化生地 | 化政历 |
人数 | 5人 | 0人 | 5人 | ... | 40人 | ... | ... |
序号 | 15 | 16 | 17 | 18 | 19 | 20 | |
组合学科 | 化政地 | 化历地 | 生政历 | 生政地 | 生历地 | 政历地 | 总计 |
人数 | ... | ... | ... | ... | ... | ... | 200人 |
为了解学生成绩与学生模拟选课情之间的关系,用分层抽样的方法从这200名学生中抽取40人的样本进行分析.
(1)样本中选择组合12号“化生历”的有多少人?样本中选择学习物理的有多少人?
(2)从样本选择学习地理且学习物理的学生中随机抽取3人,求这3人中至少有1人还要学习生物的概率;
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
【题目】标号为0到9的10瓶矿泉水.
(1)从中取4瓶,恰有2瓶上的数字相邻的取法有多少种?
(2)把10个空矿泉水瓶挂成如下4列的形式,作为射击的靶子,规定每次只能射击每列最下面的一个(射中后这个空瓶会掉到地下),把10个矿泉水瓶全部击中有几种不同的射击方案?
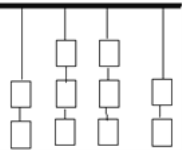
(3)把击中后的矿泉水瓶分送给A、B、C三名垃圾回收人员,每个瓶子1角钱.垃圾回收人员卖掉瓶子后有几种不同的收入结果?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工企业2018年年底投入100万元,购入一套污水处理设备。该设备每年的运转费用是0.5万元,此外,每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元。设该企业使用该设备![]() 年的年平均污水处理费用为
年的年平均污水处理费用为![]() (单位:万元)
(单位:万元)
(1)用![]() 表示
表示![]() ;
;
(2)当该企业的年平均污水处理费用最低时,企业需重新更换新的污水处理设备。则该企业几年后需要重新更换新的污水处理设备。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若a=0时,求函数![]() 的零点;
的零点;
(2)若a=4时,求函数![]() 在区间[2,5]上的最大值和最小值;
在区间[2,5]上的最大值和最小值;
(3)当![]() 时,不等式
时,不等式![]() 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某幼儿园雏鹰班的生活老师统计2018年上半年每个月的20日的昼夜温差![]() ,
,![]() 和患感冒的小朋友人数(
和患感冒的小朋友人数(![]() /人)的数据如下:
/人)的数据如下:
温差 |
|
|
|
|
|
|
患感冒人数 | 8 | 11 | 14 | 20 | 23 | 26 |
其中![]() ,
,![]() ,
,![]() .
.
(Ⅰ)请用相关系数加以说明是否可用线性回归模型拟合![]() 与
与![]() 的关系;
的关系;
(Ⅱ)建立![]() 关于
关于![]() 的回归方程(精确到
的回归方程(精确到![]() ),预测当昼夜温差升高
),预测当昼夜温差升高![]() 时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
时患感冒的小朋友的人数会有什么变化?(人数精确到整数)
参考数据:![]() .参考公式:相关系数:
.参考公式:相关系数: ,回归直线方程是
,回归直线方程是![]() ,
, ,
,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运会举办地,目前德国汉堡,美国波士顿等申办城市因市民担心赛事费用超支而相继退出,某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 80 | ||
年龄大于50岁 | 10 | ||
合计 | 70 | 100 |
(1)根据已知数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运有关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位教师的概率.
附:![]() ,
,![]() ,
,
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com