
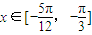 ,则
,则 的最大值为 .
的最大值为 . 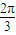 )=cot[
)=cot[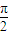 +(x+
+(x+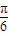 )]=tan(x+
)]=tan(x+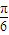 )变形,再利用同角三角函数间的基本关系将两项切化弦,通分并利用同分母分数的加法法则计算,分子利用同角三角函数间的基本关系化简,分母利用二倍角的正弦函数公式化简,分母化为一个角的正弦函数,分子化为常数,由x的范围求出这个角的范围,根据正弦函数的增减性得出正弦函数的最小值,即可得到y的最大值.
)变形,再利用同角三角函数间的基本关系将两项切化弦,通分并利用同分母分数的加法法则计算,分子利用同角三角函数间的基本关系化简,分母利用二倍角的正弦函数公式化简,分母化为一个角的正弦函数,分子化为常数,由x的范围求出这个角的范围,根据正弦函数的增减性得出正弦函数的最小值,即可得到y的最大值.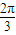 )-tan(x+
)-tan(x+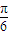 )
)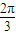 )-cot(x+
)-cot(x+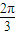 )
)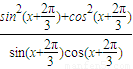
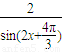 ,
,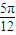 ,-
,-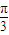 ],∴2x+
],∴2x+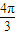 ∈[
∈[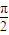 ,
,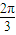 ],
],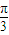 ,即2x+
,即2x+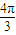 =
=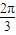 时,sin(2x+
时,sin(2x+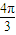 )最小值为
)最小值为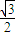 ,
,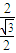 =
=
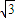 .
.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com