
【题目】在四棱锥P﹣ABCD中,底面ABCD是边长为1的正方形,PA⊥平面ABCD,PA=AB,M,N分别为PB,AC的中点, 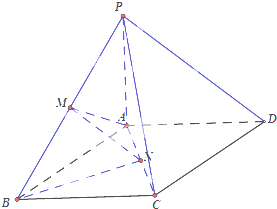
(1)求证:MN∥平面PAD;
(2)求点B到平面AMN的距离.
【答案】
(1)证明:连接BD,

则BD∩AC=N
∵M,N分别为PB,AC的中点,
∴MN是△BPD的中位线
∴MN∥PD
∵MN平面PAD,PD平面PAD
∴MN∥平面PAD
(2)解:设点B到平面AMN的距离为h,则
∵底面ABCD是边长为1的正方形,PA⊥平面ABCD,PA=AB,
∴AM=AN= ![]() ,MN=
,MN= ![]()
∴ ![]()
∵ ![]() ,M到平面ABN的距离为
,M到平面ABN的距离为 ![]()
∴由VM﹣ABN=VB﹣AMN,可得 ![]()
∴h= ![]() ,即点B到平面AMN的距离为
,即点B到平面AMN的距离为 ![]() .
.
【解析】(1)连接BD,则BD∩AC=N,利用三角形中位线的性质,可得MN∥PD,利用线面平行的判定,即可得到MN∥平面PAD;(2)利用VM﹣ABN=VB﹣AMN,可求点B到平面AMN的距离.
【考点精析】认真审题,首先需要了解直线与平面平行的判定(平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行).


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】某校初三(1)班、(2)班各有49名学生,两班在一次数学测验中的成绩统计如下表: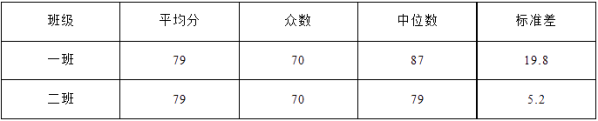
(1)请你对下面的一段话给予简要分析:
高一(1)班的小刚回家对妈妈说:“昨天的数学测验,全班平均分为79分,得70分的人最多,我得了85分,在班里算上上游了!”
(2)请你根据表中的数据,对这两个班的数学测验情况进行简要分析,并提出建议.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(ωx+φ)(ω>0,﹣π<φ<0)在区间 ![]() 上单调递增,且函数值从﹣2增大到0.若
上单调递增,且函数值从﹣2增大到0.若 ![]() ,且f(x1)=f(x2),则f(x1+x2)=( )
,且f(x1)=f(x2),则f(x1+x2)=( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=x2+bx+c为偶函数,曲线y=f(x)过点(2,5),g(x)=(x+a)f(x).
(1)求曲线y=g(x)有斜率为0的切线,求实数a的取值范围;
(2)若当x=﹣1时函数y=g(x)取得极值,确定y=g(x)的单调区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com