
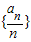 中任意一项的值均未在该数列中重复出现无数次.求a1应满足的条件.
中任意一项的值均未在该数列中重复出现无数次.求a1应满足的条件.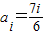 时和当
时和当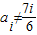 时,数列
时,数列 是否满足题中条件,便可求出a1应满足的条件.
是否满足题中条件,便可求出a1应满足的条件.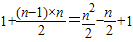 .(3分)
.(3分)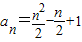 .(4分)
.(4分)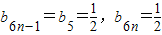
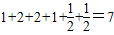 (n≥1),
(n≥1),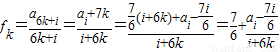 ,
,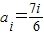 时,对任意的n=6k+i有
时,对任意的n=6k+i有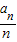 =
= ;(10分)
;(10分)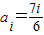 ,i∈{1,2,3,4,5,6}知
,i∈{1,2,3,4,5,6}知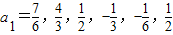 ;
; 重复出现无数次.
重复出现无数次.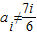 时,
时,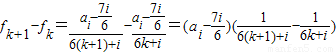 =
=
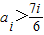 ,则对任意的k∈N有fk+1<fk,所以数列
,则对任意的k∈N有fk+1<fk,所以数列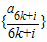 为单调减数列;
为单调减数列;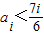 ,则对任意的k∈N有fk+1>fk,所以数列
,则对任意的k∈N有fk+1>fk,所以数列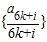 为单调增数列;
为单调增数列;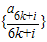 (i=1,2,3,4,5,6)均为单调数列,任意一个数在这6个数列中最多各出现一次,
(i=1,2,3,4,5,6)均为单调数列,任意一个数在这6个数列中最多各出现一次,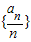 中任意一项的值最多出现六次.
中任意一项的值最多出现六次.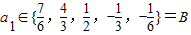 时,数列
时,数列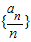 中必有某数重复出现无数次.
中必有某数重复出现无数次.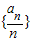 中任意一项的值均未在该数列中重复出现无数次.(14分)
中任意一项的值均未在该数列中重复出现无数次.(14分)

 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源: 题型:
| an | n |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com