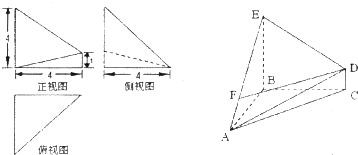
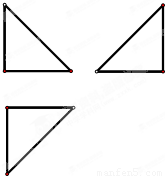
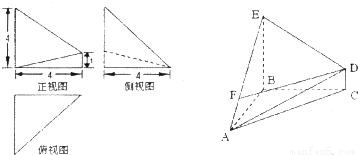
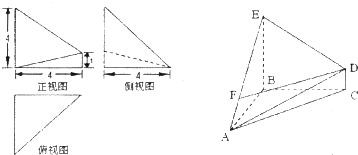
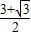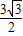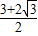解:(I)由该几何体的三视图知AB⊥平面BCDE,且BE=BC=BA=4,DC=1
∴S
△BCD=

•(4+1)•4=10
∴V
A-BCD=

•S
△BCD•AC=

即该几何体的体积为

(II)在BE上取一点G,使EG=3GB,连接DG,FG
∵EF=3FA
∴FG∥AB
又CD=1=BG
∴GD∥BC
∵GF、GD、BA、BC分别是平面GFD,平面BAC内的两条相交直线
∴平面GFD∥平面BAC
又FD?平面GFD
∴FD∥平面BAC
(III)取BC的中点O,过O作OQ⊥DE于Q,则点Q满足条件,证明如下:
连接E0,OD,BQ,AQ,CQ,在Rt△EBO和Rt△OCD中
∵
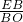
=

=2,
∴Rt△EBO∽Rt△OCD
∴∠EOB=∠ODC
∴∠EOD=90°
又OE=
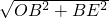
=2

,
OD=
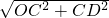
=

,ED=5
∴OQ=

=2
∴以O为圆心,以BC为直径的圆与DE相切于点Q
∴BQ⊥CQ
又CQ⊥平面BCDE,CQ?平面BCDE
∴CQ⊥AB
∴CQ⊥平面ABQ
又AQ?平面ABQ
∴CQ⊥AQ
故在棱DE上存在点使得AQ丄CQ.
分析:(I)由三视图知几何体是一个四棱锥,根据所给的数据和关系AB⊥平面BCDE,且BE=BC=BA=4,DC=1,得到体积
(II)做出辅助线,根据两个平面上的两条相交直线分别平行得到两个平面平行,根据两个平面平行的性质定理得到结论.
(III)先写出结论,取BC的中点O,过O作OQ⊥DE于Q,则点Q满足条件,下面根据两个直角三角形相似和线面垂直证明结论成立.
点评:本题考查空间中线面之间的关系和体积的求法,本题是一个综合题目,解题的关键是看出所给的三视图还原出的几何体各个部分的数据.

 •(4+1)•4=10
•(4+1)•4=10 •S△BCD•AC=
•S△BCD•AC=

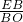 =
= =2,
=2,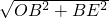 =2
=2 ,
,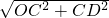 =
= ,ED=5
,ED=5 =2
=2