
【题目】在空间四边形ABCD的边AB,BC,CD,DA上分别取点E,F,G,H,如果EH,FG相交于一点M,那么M一定在直线________上.
 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:
【题目】甲、乙两人各射击一次,击中目标的概率分别是 ![]() 和
和 ![]() .假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
.假设两人射击是否击中目标,相互之间没有影响;每人各次射击是否击中目标,相互之间也没有影响.
(1)求甲射击4次,至少1次未击中目标的概率;
(2)求两人各射击4次,甲恰好击中目标2次且乙恰好击中目标3次的概率;
(3)假设某人连续2次未击中目标,则停止射击.问:乙恰好射击5次后,被中止射击的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}中公差d≠0,有a1+a4=14,且a1,a2,a7成等比数列.
(Ⅰ)求{an}的通项公式an与前n项和公式Sn;
(Ⅱ)令bn=![]() (k<0),若{bn}是等差数列,求数列{
(k<0),若{bn}是等差数列,求数列{![]() }的前n项和Tn.
}的前n项和Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
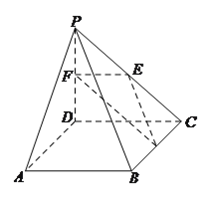
【题目】如图,在四棱锥![]() 中,
中, ![]() 是正方形,
是正方形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别是
分别是![]() ,
, ![]() ,
, ![]() 的中点.
的中点.
(![]() )求四棱锥
)求四棱锥![]() 的体积.
的体积.
(![]() )求证:平面
)求证:平面![]() 平面
平面![]() .
.
(![]() )在线段
)在线段![]() 上确定一点
上确定一点![]() ,使
,使![]() 平面
平面![]() ,并给出证明.
,并给出证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有甲,乙两个靶,某射手向甲靶射击一次,命中的概率是 ![]() ,向乙靶射击两次,每次命中的概率是
,向乙靶射击两次,每次命中的概率是 ![]() ,若该射手每次射击的结果相互独立,则该射手完成以上三次射击恰好命中一次的概率是( )
,若该射手每次射击的结果相互独立,则该射手完成以上三次射击恰好命中一次的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|﹣2.
(Ⅰ)若a=1,求不等式f(x)+|2x﹣3|>0的解集;
(Ⅱ)若关于x的不等式f(x)<|x﹣3|恒成立,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com