
| A. | 2014 | B. | 2015 | C. | 4028 | D. | 4030 |
分析 根据抽象函数的表达式,利用函数单调性的性质即可得到结论.
解答 解:∵对于任意的x1,x2∈[-2015,2015],都有f(x1+x2)=f(x1)+f(x2)-2015,
∴令x1=x2=0,得f(0)=2015,
再令x1+x2=0,将f(0)=2015代入可得f(x)+f(-x)=4030.
设x1<x2,x1,x2∈[-2015,2015],
则x2-x1>0,f(x2-x1)=f(x2)+f(-x1)-2015,
∴f(x2)+f(-x1)-2015<2015.
又∵f(-x1)=4030-f(x1),
∴可得f(x2)>f(x1),
即函数f(x)是递减的,
∴f(x)max=f(-2015),f(x)min=f(2015).
又∵f(2015)+f(-2015)=4030,
∴M+N的值为4030.
故选:D.
点评 本题主要考查函数值的计算,利用赋值法,证明函数的单调性是解决本题的关键,综合性较强,有一定的难度.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2016-2017学年湖南益阳市高二9月月考数学(理)试卷(解析版) 题型:选择题
设集合P={x∈R|x2+2x<0},Q={x∈R| 1/(x+1)>0},则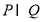 =( )
=( )
A.(﹣2,1) B.(﹣1,0) C.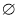 D.(﹣2,0)
D.(﹣2,0)
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 15 | B. | 25 | C. | 35 | D. | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com