
【题目】如图,三棱柱![]() 的底面是边长为
的底面是边长为![]() 的正三角形,侧棱
的正三角形,侧棱![]() 底面
底面![]() 为
为![]() 中点,
中点,![]() 分别为
分别为![]() 上的点,且满足
上的点,且满足![]() .
.

(1)求证:平面![]() 平面
平面![]() , ;
, ;
(2)若三棱锥![]() 的体积为
的体积为![]() ,求三棱柱的侧棱长.
,求三棱柱的侧棱长.
科目:高中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 若命题![]() 均为真命题,则命题
均为真命题,则命题![]() 为真命题
为真命题
B. “若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ”
”
C. 在![]() ,“
,“![]() ”是“
”是“![]() ”的充要条件
”的充要条件
D. 命题![]() “
“![]() ”的否定为
”的否定为![]() “
“![]() ”
”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() :
:![]() ,四边形
,四边形![]() 和
和![]() 都为正方形,原点
都为正方形,原点![]() 为
为![]() 的中点,点
的中点,点![]() 在抛物线
在抛物线![]() 上.
上.
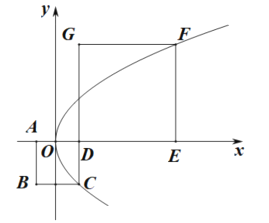
(1)求点![]() 和点
和点![]() 的坐标;
的坐标;
(2)过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次数学测验共有10道选择题,每道题共有四个选项,且其中只有一个选项是正确的,评分标准规定:每选对1道题得5分,不选或选错得0分,某考试每道都选并能确定其中有6道题能选对,其余4道题无法确定正确选项,但这4道题中有2道能排除两个错误选项,另2题只能排除一个错误选项,于是该生做这4道题时每道题都从不能排除的选项中随机挑选一个选项做答,且各题做答互不影响.
(Ⅰ)求该考生本次测验选择题得50分的概率;
(Ⅱ)求该考生本次测验选择题所得分数的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C的极坐标方程是ρ=6sinθ,建立以极点为坐标原点,极轴为x轴正半轴的平面直角坐标系.直线l的参数方程是![]() ,(t为参数).
,(t为参数).
(1)求曲线C的直角坐标方程;
(2)若直线l与曲线C相交于A,B两点,且|AB|=![]() ,求直线的斜率k.
,求直线的斜率k.
查看答案和解析>>
科目:高中数学 来源: 题型:
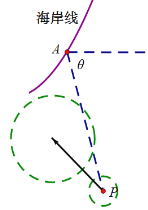
【题目】在某海滨城市附近海面有一台风,据监测,当前台风中心位于城市A(看做一点)的东偏南![]() 角方向
角方向![]() ,300 km的海面P处,并以20km / h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域,当前半径为60 km,并以10km / h的速度不断增大.
,300 km的海面P处,并以20km / h的速度向西偏北45°方向移动.台风侵袭的范围为圆形区域,当前半径为60 km,并以10km / h的速度不断增大.
(1) 问10小时后,该台风是否开始侵袭城市A,并说明理由;
(2) 城市A受到该台风侵袭的持续时间为多久?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,
,![]() 满足
满足![]() (
(![]() …).
…).
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() 且
且![]() ,则数列
,则数列![]() 中第几项最小?请说明理由;
中第几项最小?请说明理由;
(3)若![]() (n=1,2,3,…),求证:“数列
(n=1,2,3,…),求证:“数列![]() 为等差数列”的充分必要条件是“数列
为等差数列”的充分必要条件是“数列![]() 为等差数列且
为等差数列且![]() (n=1,2,3,…)”.
(n=1,2,3,…)”.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据阅兵领导小组办公室介绍,2019年国庆70周年阅兵有59个方(梯)队和联合军乐团,总规模约1.5万人,是近几次阅兵中规模最大的一次.其中,徒步方队15个.为了保证阅兵式时队列保持整齐,各个方队对受阅队员的身高也有着非常严格的限制,太高或太矮都不行.徒步方队队员,男性身高普遍在175cm至185cm之间;女性身高普遍在163cm至175cm之间,这是常规标准.要求最为严格的三军仪仗队,其队员的身高一般都在184cm至190cm之间.经过随机调查某个阅兵阵营中女子100人,得到她们身高的直方图,如图,记C为事件:“某一阅兵女子身高不低于169cm”,根据直方图得到P(C)的估计值为0.5.
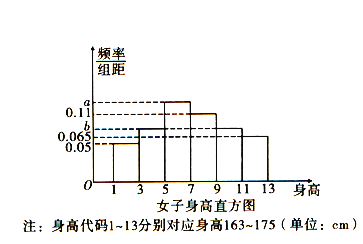
(1)求直方图中a,b的值;
(2)估计这个阵营女子身高的平均值 (同一组中的数据用该组区间的中点值为代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() 为常数) .
为常数) .
(1)当![]() 时,求曲线
时,求曲线![]() 在
在![]() 处的切线方程:
处的切线方程:
(2)若函数![]() 在
在![]() 内存在唯一极值点
内存在唯一极值点![]() ,求实数
,求实数![]() 的取值范围,并判断
的取值范围,并判断![]() ,是
,是![]() 在
在![]() 内的极大值点还是极小值点.
内的极大值点还是极小值点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com