
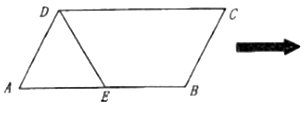
【题目】已知平行四边形![]() 中,
中,![]() ,
,![]() 为
为![]() 的中点,且△
的中点,且△![]() 是等边三角形,沿
是等边三角形,沿![]() 把△
把△![]() 折起至
折起至![]() 的位置,使得
的位置,使得![]() .
.
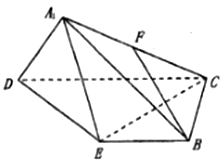
(1)![]() 是线段
是线段![]() 的中点,求证:
的中点,求证:![]() 平面
平面![]() ;
;
(2)求证:![]() ;
;
(3)求点![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)取![]() 的中点
的中点![]() ,连结
,连结![]() 、
、![]() ,可证
,可证![]() ,且
,且![]() ,结合条件可得四边形
,结合条件可得四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,由线面平行的判定定理即可得到
,由线面平行的判定定理即可得到![]() 平面
平面![]() ;(2)由折叠前图形可得
;(2)由折叠前图形可得![]() ,在四棱锥
,在四棱锥![]() 中,即有
中,即有![]() ,由余弦定理和勾股定理可得
,由余弦定理和勾股定理可得![]() ,从而证得
,从而证得![]() 平面
平面![]() ,由线面垂直的性质可证得结论;(3)设点
,由线面垂直的性质可证得结论;(3)设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,进行定体积变换
,进行定体积变换![]() 即可求得点
即可求得点![]() 到平面
到平面![]() 的距离.
的距离.
试题解析:证明:(1)取![]() 的中点
的中点![]() ,连结
,连结![]() 、
、![]() ,
,
因为![]() 为
为![]() 的中点,故
的中点,故![]() ,且
,且![]() ,
,
又![]() ,且
,且![]()
所以四边形![]() 为平行四边形,
为平行四边形,![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.
(2)折叠前,![]() ,
,![]() ,即
,即![]() ,
,
在四棱锥![]() 中,即有
中,即有![]() ,
,
在△![]() 中,
中,![]() ,
,![]() ,由余弦定理得
,由余弦定理得![]() ,
,
又![]() ,
,![]() ,由勾股定理的逆定理,得
,由勾股定理的逆定理,得![]() ,
,![]() ,
,
又![]() ,从而
,从而![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,得
,得![]() .
.
(3)由(2)知,![]() 平面
平面![]() ,
,
设点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则由
,则由![]() ,
,
得![]() ,
,![]() ,
,
解得![]() .
.


科目:高中数学 来源: 题型:
【题目】某校高一(1)班有男同学45名,女同学15名,老师按照分层抽样的方法抽取4人组建了一个课外兴趣小组.
(I)求课外兴趣小组中男、女同学的人数;
(II)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是从小组里选出一名同学做实验,该同学做完后,再从小组内剩下的同学中选出一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
(III)在(II)的条件下,第一次做实验的同学A得到的实验数据为38,40,41,42,44,第二次做实验的同学B得到的实验数据为39,40,40,42,44,请问哪位同学的实验更稳定?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知向量a=(cos α,sin α),b=(cos β,sin β),c=(-1,0).
(1) 求向量b+c的模的最大值;
(2) 若α=![]() ,且a⊥(b+c),求cos β的值.
,且a⊥(b+c),求cos β的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(ax2-x+1)(a>0,a≠1).
(1) 若a=![]() ,求函数f(x)的值域.
,求函数f(x)的值域.
(2) 当f(x)在区间![]() 上为增函数时,求a的取值范围.
上为增函数时,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:某污水处理厂要在一个矩形污水处理池(![]() )的池底水平铺设污水净化管道(
)的池底水平铺设污水净化管道(![]() 是直角顶点)来处理污水,管道越长污水净化效果越好,设计要求管道的的接口
是直角顶点)来处理污水,管道越长污水净化效果越好,设计要求管道的的接口![]() 是
是![]() 的中点,
的中点,![]() 分别落在线段
分别落在线段![]() 上。已知
上。已知![]() 米,
米,![]() 米,记
米,记![]() .
.
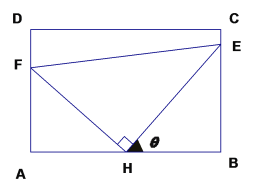
(1)试将污水净化管道的长度![]() 表示为
表示为![]() 的函数,并写出定义域;
的函数,并写出定义域;
(2)若![]() ,求此时管道的长度
,求此时管道的长度![]() ;
;
(3)当![]() 取何值时,污水净化效果最好?并求出此时管道的长度。
取何值时,污水净化效果最好?并求出此时管道的长度。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分12分)已知![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() ,当
,当![]()
![]() ,
,![]() 时,有
时,有![]() 成立.
成立.
(Ⅰ)判断![]() 在
在![]() 上的单调性,并加以证明;
上的单调性,并加以证明;
(Ⅱ)若![]() 对所有的
对所有的![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏,将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.
(1)若将一般等级和良好等级合称为合格等级,根据已知条件完成下面的![]() 列联表,并据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?
列联表,并据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关?
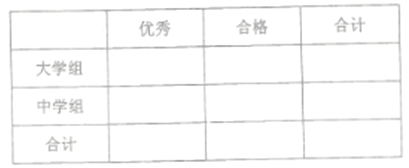


(2)若参赛选手共6万人,用频率估计概率,试估计其中优秀等级的选手人数;
(3)在优秀等级的选手中取6名,依次编号为1,2,3,4,5,6,在良好等级的选手中取6名,依次编号为1,2,3,4,5,6,在选出的6名优秀等级的选手中任取一名,记其编号为![]() ,在选出的6名良好等级的选手中任取一名,记其编号为
,在选出的6名良好等级的选手中任取一名,记其编号为![]() ,求使得方程组
,求使得方程组![]() 有唯一一组实数解
有唯一一组实数解![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数(Air Quality Index,简称![]() )是定量描述空气质量状况的指数,空气质量按照
)是定量描述空气质量状况的指数,空气质量按照![]() 大小分为六级,
大小分为六级,![]() 为优;
为优;![]() 为轻度污染;
为轻度污染;![]() 为中度污染;
为中度污染;![]() 为重度污染;
为重度污染;![]() 为严重污染.一环保人士记录去年某地某月10天的
为严重污染.一环保人士记录去年某地某月10天的![]() 的茎叶图如右.
的茎叶图如右.
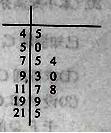
(1)利用该样本估计该地本月空气质量优良(![]() )的天数;(按这个月总共30天计算)
)的天数;(按这个月总共30天计算)
(2)将频率视为概率,从本月中随机抽取3天,记空气质量优良的天数为![]() ,求
,求![]() 的概率分布列和数学期望.
的概率分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在五棱锥![]() 中,平面
中,平面![]() 平面
平面![]() ,且
,且![]() .
.
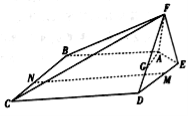
(1)已知点![]() 在线段
在线段![]() 上,确定
上,确定![]() 的位置,使得
的位置,使得![]() 平面
平面![]() ;
;
(2)点![]() 分别在线段
分别在线段![]() 上,若沿直线
上,若沿直线![]() 将四边形
将四边形![]() 向上翻折,
向上翻折,![]() 与
与![]() 恰好重合,求直线
恰好重合,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com