练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列说法正确的个数有_________

    （1）已知变量和满足关系，则与正相关；（2）线性回归直线必过点 ；

    （3）对于分类变量与的随机变量，越大说明“与有关系”的可信度越大

    （4）在刻画回归模型的拟合效果时，残差平方和越小，相关指数的值越大，说明拟合的效果越好.

    【答案】3个

    【解析】

    直接利用线性回归直线的相关理论知识的应用求出结果．

    （1）已知变量x和y满足关系y=-2x+3，则x与y正相关；应该是：x与y负相关．故错误.
    （2）线性回归直线必过点，线性回归直线必过中心点．故正确．
    （3）对于分类变量A与B的随机变量，越大说明“A与B有关系”的可信度越大．
    根据课本上有原句，故正确．
    （4）在刻画回归模型的拟合效果时，残差平方和越小，相关指数R2的值越大，说明拟合的效果越好．故正确，根据课本上有原句．
    故填3个．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知椭圆过点，且两焦点与短轴的一个顶点的连线构成等腰直角三角形.

    （Ⅰ）求椭圆的方程；

    （Ⅱ）过的直线交椭圆于，两点，试问：是否存在一个定点，使得以为直径的圆恒过点？若存在，求出点的坐标；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】高尔顿（钉）板是在一块竖起的木板上钉上一排排互相平行、水平间隔相等的圆柱形铁钉（如图），并且每一排钉子数目都比上一排多一个，一排中各个钉子恰好对准上面一排两相邻铁钉的正中央.从入口处放入一个直径略小于两颗钉子间隔的小球，当小球从两钉之间的间隙下落时，由于碰到下一排铁钉，它将以相等的可能性向左或向右落下，接着小球再通过两铁钉的间隙，又碰到下一排铁钉.如此继续下去，在最底层的5个出口处各放置一个容器接住小球.

    （Ⅰ）理论上，小球落入4号容器的概率是多少？

    （Ⅱ）一数学兴趣小组取3个小球进行试验，设其中落入4号容器的小球个数为，求的分布列与数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列中，，且对任意正整数都成立，数列的前项和为.

    （1）若，且，求；

    （2）是否存在实数k，使数列是公比不为1的等比数列，且任意相邻三项按某顺序排列后成等差数列，若存在，求出所有k的值；若不存在，请说明理由；

    （3）若，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】俗话说“三个臭皮匠，顶个诸葛亮”，从数学角度解释这句话的含义.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为迎接年北京冬季奥运会，普及冬奥知识，某校开展了“冰雪答题王”冬奥知识竞赛活动．现从参加冬奥知识竞赛活动的学生中随机抽取了名学生，将他们的比赛成绩（满分为分）分为组：，，，，，，得到如图所示的频率分布直方图．

    （Ⅰ）求的值；

    （Ⅱ）记表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生，该学生的比赛成绩不低于分”，估计的概率；

    （Ⅲ）在抽取的名学生中，规定：比赛成绩不低于分为“优秀”，比赛成绩低于分为“非优秀”．请将下面的列联表补充完整，并判断是否有的把握认为“比赛成绩是否优秀与性别有关”？

    优秀

    非优秀

    合计

    男生

    女生

    合计

    参考公式及数据：，．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

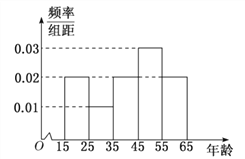
    【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题，拟定出台“延迟退休年龄政策”.为了了解人们]对“延迟退休年龄政策”的态度，责成人社部进行调研.人社部从网上年龄在1565岁的人群中随机调查100人，调査数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下：

    年龄

    支持“延迟退休”的人数

    15

    5

    15

    28

    17

    （1）由以上统计数据填列联表，并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异；

    45岁以下

    45岁以上

    总计

    支持

    不支持

    /td>

    总计

    （2）若以45岁为分界点，从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动.现从这8人中随机抽2人

    ①抽到1人是45岁以下时，求抽到的另一人是45岁以上的概率.

    ②记抽到45岁以上的人数为，求随机变量的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某班50位学生期中考试数学成绩的频率分布直方图如图所示，其中成绩分组区间是：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]

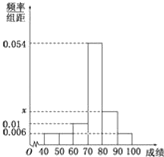
    （Ⅰ）求图中的值，并估计该班期中考试数学成绩的众数；

    （Ⅱ）从成绩不低于90分的学生和成绩低于50分的学生中随机选取2人，求这2人成绩均不低于90分的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了解全市统考情况，从所有参加考试的考生中抽取4000名考生的成绩，频率分布直方图如下图所示.

    （1）求这4000名考生的半均成绩（同一组中数据用该组区间中点作代表）；

    （2）由直方图可认为考生考试成绩z服从正态分布，其中分别取考生的平均成绩和考生成绩的方差，那么抽取的4000名考生成绩超过84.81分（含84.81分）的人数估计有多少人？

    （3）如果用抽取的考生成绩的情况来估计全市考生的成绩情况，现从全市考生中随机抽取4名考生，记成绩不超过84.81分的考生人数为，求.（精确到0.001）

    附：①；

    ②，则；

    ③.

    查看答案和解析>>

    同步练习册答案