
·ÖĪö £Ø¢ń£©ĄūÓĆ×éŗĻÖŖŹ¶Č·¶Ø»ł±¾ŹĀ¼žµÄøöŹż£¬Č»ŗóĄūÓĆ¹ÅµäøÅŠĶøÅĀŹ¼ĘĖć¹«Ź½µĆ“š°ø£»
£Ø¢ņ£©Ė껜±äĮæXµÄĖłÓŠæÉÄÜȔֵĪŖ0£¬1£¬2£¬3£¬4£¬ÓɹŵäøÅŠĶøÅĀŹ¼ĘĖć¹«Ź½ĒóµĆøÅĀŹ£¬ĮŠ³ö·Ö²¼ĮŠ£¬“śČėĘŚĶū¹«Ź½ĒóĘŚĶū£®
½ā“š ½ā£ŗ£Ø¢ń£©ÓÉŅŃÖŖÓŠ$P£ØA£©=\frac{C_2^2C_7^2+C_3^2C_7^2}{{C_{12}^4}}=\frac{28}{165}$£¬
ĖłŅŌŹĀ¼žA·¢ÉśµÄøÅĀŹĪŖ$\frac{28}{165}$£®
£Ø¢ņ£©XµÄĖłÓŠæÉÄÜȔֵĪŖ0£¬1£¬2£¬3£¬4£¬
$P£ØX=0£©=\frac{C_5^0C_7^4}{{C_{12}^4}}=\frac{7}{99}$£¬$P£ØX=1£©=\frac{C_5^1C_7^3}{{C_{12}^4}}=\frac{35}{99}$£¬
$P£ØX=2£©=\frac{C_5^2C_7^2}{{C_{12}^4}}=\frac{14}{33}$£¬$P£ØX=3£©=\frac{C_5^3C_7^1}{{C_{12}^4}}=\frac{14}{99}$£¬$P£ØX=4£©=\frac{C_5^4}{{C_{12}^4}}=\frac{1}{99}$
ĖłŅŌĖ껜±äĮæXµÄ·Ö²¼ĮŠĪŖ
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{7}{99}$ | $\frac{35}{99}$ | $\frac{14}{33}$ | $\frac{14}{99}$ | $\frac{1}{99}$ |
µćĘĄ æ¼µćÅÅĮŠ×éŗĻ”¢¹ÅµäøÅŠĶ”¢Ė껜±äĮæµÄ·Ö²¼ĮŠ¼°ŹżŃ§ĘŚĶū£®æ¼²éŌĖÓĆøÅĀŹÖŖŹ¶½ā¾ö¼ņµ„Źµ¼ŹĪŹĢāµÄÄÜĮ¦£¬ŹĒÖŠµµĢā£®


 Š”ѧæĪŹ±ĢŲѵĻµĮŠ“š°ø
Š”ѧæĪŹ±ĢŲѵĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | µŚŅ»ĻóĻŽ | B£® | µŚ¶žĻóĻŽ | C£® | µŚČżĻóĻŽ | D£® | µŚĖÄĻóĻŽ |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
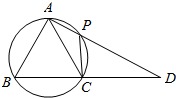 ČēĶ¼ĖłŹ¾£¬ŌŚĖıߊĪABCPÖŠ£¬Ļ߶ĪAPÓėBCµÄŃÓ³¤Ļß½»ÓŚµćD£¬ŅŃÖŖAB=ACĒŅA£¬B£¬C£¬PĖÄµć¹²Ō²£®
ČēĶ¼ĖłŹ¾£¬ŌŚĖıߊĪABCPÖŠ£¬Ļ߶ĪAPÓėBCµÄŃÓ³¤Ļß½»ÓŚµćD£¬ŅŃÖŖAB=ACĒŅA£¬B£¬C£¬PĖÄµć¹²Ō²£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
| A£® | -2 | B£® | -1 | C£® | 0 | D£® | 1 |
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com