解:(1)当x=y=0时,f(0)=f(0)•f(0),∴f(0)=0,f(0)=1
若f(0)=0,则得f(x)=f(x+0)=f(x)f(0)=0,不可能,舍去
∴f(0)=1
当x>0时,f(x)=
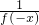
<1,得,0<f(x)<1
∴f(x)>0,x∈R
若x<y,则,x-y<0,f(x-y)>1,f(x)=f(x-y)•f(y)>f(y),
∴f(x)-f(y)>0,
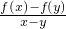
<0
同理,若x>y,
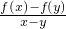
<0∴任意x,y∈R,x≠y,都有
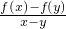
<0
(2)∵g(1)=f(0)=1,g(2)=f(-2)=f(-1)f(-1)=5
由(1)可得f(x)为单调减函数∵f[g(n+2)]=
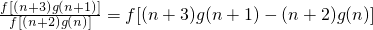
∴g(n+2)=(n+3)g(n+1)-(n+2)g(n)
得∴g(n+2)-g(n+1)=(n+2)(g(n+1)-g(n)),n≥1
∴g(n)-g(n-1)=n(g(n-1)-g(n-2)),n≥3g(n-1)-g(n-2)=(n-1)(g(n-2)-g(n-3))
…g(3)-g(2)=3(g(2)-g(1))
相乘得:∴g(n)-g(n-1)=
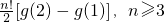
…①
又由①式得:g(n)-g(n-1)=
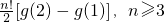
g(n-1)-g(n-2)=
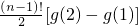
…g(3)-g(2)=
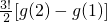
,g(2)-g(1)=
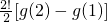
相加得:g(n)-g(1)=
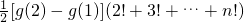
,n≥2,
g(n)=2(2!+3!+…+n!)+1,n≥2,
g(1)=1,g(2)=5,g(3)=17,g(4)=65,g(5)=305,
g(6)=1745,g(7)=11825,g(8)=92465,g(9)=818225,
由于当n≥10时,n!能被25整除
综上,存在正整数n,当n=7或n≥9,n∈N时,g(n)是25的倍数.
分析:(1)利用赋值法,当x=y=0时,f(0)=f(0)•f(0),得出f(0)=1;再利用条件当x>0时,f(x)=
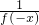
<1,得对任意实数都有f(x)>0,再对x,y的大小关系进行分类讨论:若x<y,则f(x)=f(x-y)•f(y)>f(y),从而f(x)-f(y)>0;同理,若x>y,
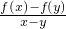
<0得证;
(2)对于存在性问题,可先假设存在,即存在正整数n,使得g(n)是25的倍数,再利用函数的单调性结合数列的质,求出g(n)的表达式,若出现矛盾,则说明假设不成立,即不存在;否则存在.
点评:本题是一个抽象函数题,其解答过程中用到了数列中的累加法累乘法,可归为数列与函数综合,解答过程中出现了阶乘,此符号题中有定义,考点中可不考虑.

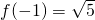 ;
;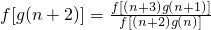 ,n∈N*
,n∈N*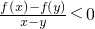 ;
;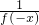 <1,得,0<f(x)<1
<1,得,0<f(x)<1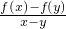 <0
<0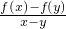 <0∴任意x,y∈R,x≠y,都有
<0∴任意x,y∈R,x≠y,都有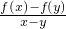 <0
<0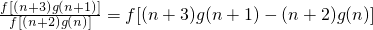
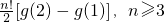 …①
…①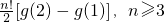 g(n-1)-g(n-2)=
g(n-1)-g(n-2)=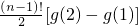
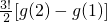 ,g(2)-g(1)=
,g(2)-g(1)=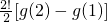
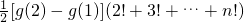 ,n≥2,
,n≥2,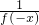 <1,得对任意实数都有f(x)>0,再对x,y的大小关系进行分类讨论:若x<y,则f(x)=f(x-y)•f(y)>f(y),从而f(x)-f(y)>0;同理,若x>y,
<1,得对任意实数都有f(x)>0,再对x,y的大小关系进行分类讨论:若x<y,则f(x)=f(x-y)•f(y)>f(y),从而f(x)-f(y)>0;同理,若x>y,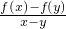 <0得证;
<0得证;

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案