
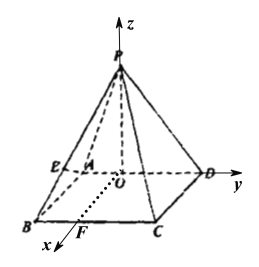
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为3的疋方形,侧面
是边长为3的疋方形,侧面![]() 与底面
与底面![]() 垂直,过点
垂直,过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,且满足
,且满足![]() ,点
,点![]() 在棱
在棱![]() 上,
上,![]()
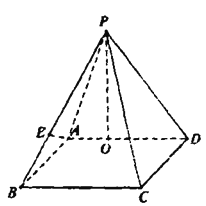
(1)当![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(2)当![]() 取何值时,二面角
取何值时,二面角![]() 的正弦值为
的正弦值为![]() .
.
【答案】(1)![]() .(2)
.(2)![]()
【解析】
在底面![]() 内过点
内过点![]() 作
作![]() ,
,![]() 交
交![]() 与
与![]() ,由已知可证
,由已知可证![]() 底面
底面![]() ,建立空间直角坐标系,求出
,建立空间直角坐标系,求出![]() 坐标.
坐标.
(1)由条件得出![]() 坐标,求出平面
坐标,求出平面![]() 法向量,根据向量的线面角公式,即可求解;
法向量,根据向量的线面角公式,即可求解;
(2)设![]() ,分别求出平面
,分别求出平面![]() 、平面
、平面![]() 的法向量,根据向量的面面角公式,结合已知,得到关于
的法向量,根据向量的面面角公式,结合已知,得到关于![]() 的方程,求解即可得出结论
的方程,求解即可得出结论
解:因为侧面![]() 底面
底面![]() ,
,
![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 平面
平面![]() ,
,
所以![]() 底面
底面![]() ,
,
在底面![]() 内过点
内过点![]() 作
作![]() ,
,
![]() 交
交![]() 与
与![]() ,则
,则![]() ,
,
又![]() 底面
底面![]() ,
,
所以![]() ,
,![]() ,
,
以![]() ,
,![]() ,
,![]() 为
为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
![]() ,
,
(1)点![]() ,因为
,因为![]() ,
,
所以点![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
满足 ,
,
取![]() ,法向量为
,法向量为![]() ,
,
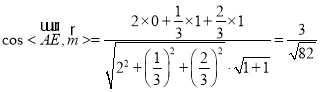 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(2)设![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
满足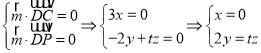 ,
,
取![]() ,法向量为
,法向量为![]() ,
,
![]()
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
满足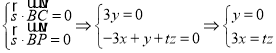 ,
,
取![]() ,法向量
,法向量![]() ,
,
由题意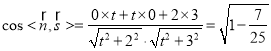
整理得![]() ,
,![]() ,
,
![]() ,即
,即![]() .
.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,倾斜角为
中,倾斜角为![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).在以坐标原点为极点,
为参数).在以坐标原点为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的倾斜角.
的倾斜角.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】进位制是人们为了计数和运算方便而约定的计数系统,“满几进一”就是几进制,不同进制之间可以相互转化,例如把十进制的89转化为二进制,根据二进制数“满二进一”的原则,可以用2连续去除89得商,然后取余数,具体计算方法如下:
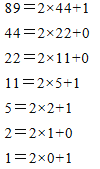
把以上各步所得余数从下到上排列,得到89=1011001(2)这种算法叫做“除二取余法”,上述方法也可以推广为把十进制数化为k进制数的方法,称为“除k取余法”,那么用“除k取余法”把89化为七进制数为_.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱![]() 中,
中,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,
,![]() ,点D是侧棱
,点D是侧棱![]() 上的一点.
上的一点.
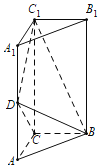
(1)证明:当点D是![]() 的中点时,
的中点时,![]() 平面BCD;
平面BCD;
(2)若二面角![]() 的余弦值为
的余弦值为![]() 求二面角
求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月![]() ,
,![]() 两种移动支付方式的使用情况,从全校学生随机抽取了100人,发现使用
两种移动支付方式的使用情况,从全校学生随机抽取了100人,发现使用![]() 或
或![]() 支付方式的学生共有90人,使用
支付方式的学生共有90人,使用![]() 支付方式的学生共有70人,
支付方式的学生共有70人,![]() ,
,![]() 两种支付方式都使用的有60人,则该校使用
两种支付方式都使用的有60人,则该校使用![]() 支付方式的学生人数与该校学生总数比值的估计值为______.
支付方式的学生人数与该校学生总数比值的估计值为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com