
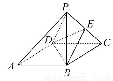
如图所示,底面为平行四边形ABCD的四棱锥P-ABCD中,E为PC的中点.求证:PA∥平面BDE.(要求注明每一步推理的大前提、小前提和结论,并最终把推理过程用简略的形式表示出来)
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十四第五章第五节练习卷(解析版) 题型:选择题
已知数列{an}满足:a1=1,an>0,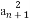 -
-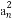 =1(n∈N*),那么使an<5成立的n的最大值为( )
=1(n∈N*),那么使an<5成立的n的最大值为( )
(A)4(B)5(C)24(D)25
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十五第六章第一节练习卷(解析版) 题型:填空题
已知-3<b<a<-1,-2<c<-1,则(a-b)c2的取值范围是 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十二第五章第三节练习卷(解析版) 题型:选择题
数列{an}是公差不为0的等差数列,且a1,a3,a7为等比数列{bn}的连续三项,则数列{bn}的公比为( )
(A)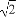 (B)4(C)2(D)
(B)4(C)2(D)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:填空题
观察下列等式:13+23=32,13+23+33=62,13+23+33+43=102,…,根据上述规律,第五个等式为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十九第六章第五节练习卷(解析版) 题型:选择题
推理“①矩形是平行四边形;②正方形是矩形;③正方形是平行四边形”中的小前提是( )
(A)① (B)②
(C)③ (D)以上均错
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业三十三第五章第四节练习卷(解析版) 题型:选择题
数列{an}的前n项和为Sn,若an=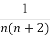 ,则S10等于( )
,则S10等于( )
(A) (B)
(B) (C)
(C) (D)
(D)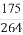
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业七十第十章第七节练习卷(解析版) 题型:解答题
如图,电路由电池A,B,C并联组成.电池A,B,C损坏的概率分别是0.3,0.2,0.2,求电路断电的概率.
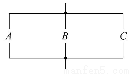
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com