
【题目】已知函数![]() ,x∈[0,
,x∈[0,![]() ],若函数F(x)=f(x)-3的所有零点依次记为
],若函数F(x)=f(x)-3的所有零点依次记为![]() ,且
,且![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
函数F(x)=f(x)﹣3的所有零点,转化为函数![]() 与y=3的交点问题,求出函数f(x)的对称轴,根据f(x)的对称性得出任意两相邻两零点的和,从而得出答案.
与y=3的交点问题,求出函数f(x)的对称轴,根据f(x)的对称性得出任意两相邻两零点的和,从而得出答案.
函数![]() ,
,
令2x![]() kπ得x
kπ得x![]() ,k∈Z,即f(x)的对称轴方程为x
,k∈Z,即f(x)的对称轴方程为x![]() ,k∈Z.
,k∈Z.
∵f(x)的最小正周期为T=π,0≤x![]() ,
,
当k=0时,可得y轴右侧第一条对称轴x![]() ,当k=28时,可得x
,当k=28时,可得x![]() ,
,
∴f(x)在[0,![]() ]上有28条对称轴,
]上有28条对称轴,
根据正弦函数的性质可知:函数![]() 与y=3的交点有29个点,即x1,x2关于
与y=3的交点有29个点,即x1,x2关于![]() 对称,x2,x3关于
对称,x2,x3关于![]() 对称,…,即x1+x2
对称,…,即x1+x2![]() 2,x2+x3
2,x2+x3![]() 2,…,x28+x29=2
2,…,x28+x29=2![]()
将以上各式相加得:x1+2x2+2x3+…+2x28+2x29+2x28+x29=2(![]() )=(2+5+8+…+83)
)=(2+5+8+…+83)![]()
故选:A.


 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为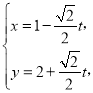 (
(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴为极轴的极坐标系中,圆
轴为极轴的极坐标系中,圆![]() 的方程
的方程![]() .
.
(1)写出直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 的直角坐标为
的直角坐标为![]() ,圆
,圆![]() 与直线
与直线![]() 交于
交于![]() 两点,求弦
两点,求弦![]() 中点
中点![]() 的直角坐标和
的直角坐标和![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C的顶点在原点,对称轴是x轴,并且经过点![]() ,抛物线C的焦点为F,准线为l.
,抛物线C的焦点为F,准线为l.
(1)求抛物线C的方程;
(2)过F且斜率为![]() 的直线h与抛物线C相交于两点A、B,过A、B分别作准线l的垂线,垂足分别为D、E,求四边形
的直线h与抛物线C相交于两点A、B,过A、B分别作准线l的垂线,垂足分别为D、E,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某餐厅通过查阅了最近5次食品交易会参会人数![]() (万人)与餐厅所用原材料数量
(万人)与餐厅所用原材料数量![]() (袋),得到如下统计表:
(袋),得到如下统计表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | |
参会人数 | 13 | 9 | 8 | 10 | 12 |
原材料 | 32 | 23 | 18 | 24 | 28 |
(1)根据所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知购买原材料的费用![]() (元)与数量
(元)与数量![]() (袋)的关系为
(袋)的关系为![]() ,
,
投入使用的每袋原材料相应的销售收入为700元,多余的原材料只能无偿返还,据悉本次交易大会大约有15万人参加,根据(1)中求出的线性回归方程,预测餐厅应购买多少袋原材料,才能获得最大利润,最大利润是多少?(注:利润![]() 销售收入
销售收入![]() 原材料费用).
原材料费用).
参考公式:  ,
, ![]() .
.
参考数据: ![]() ,
, ![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌经销商在一广场随机采访男性和女性用户各50名,其中每天玩微信超过6小时的用户列为“微信控”,否则称其为“非微信控”,调查结果如下:
微信控 | 非微信控 | 合计 | |
男性 | 26 | 24 | 50 |
女性 | 30 | 20 | 50 |
合计 | 56 | 44 | 100 |
(1)根据以上数据,能否有![]() 的把握认为“微信控”与“性别”有关?
的把握认为“微信控”与“性别”有关?
(2)现从调查的女性用户中按分层抽样的方法选出5人,再随机抽取3人赠送礼品,试求抽取3人中恰有2人是“微信控”的概率.
参考公式: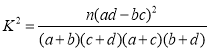 ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.040 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义域为![]() 的函数
的函数![]() 是奇函数,其中
是奇函数,其中![]() 为实数.
为实数.
(1)求实数![]() 的值;
的值;
(2)用定义证明![]() 在
在![]() 上是减函数;
上是减函数;
(3)若对于任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 过点
过点![]() ,其左右焦点分别为
,其左右焦点分别为![]() ,
,![]() ,三角形
,三角形![]() 的面积为
的面积为![]() .
.
![]() Ⅰ
Ⅰ![]() 求椭圆C的方程;
求椭圆C的方程;
![]() Ⅱ
Ⅱ![]() 已知A,B是椭圆C上的两个动点且不与坐标原点O共线,若
已知A,B是椭圆C上的两个动点且不与坐标原点O共线,若![]() 的角平分线总垂直于x轴,求证:直线AB与两坐标轴围成的三角形一定是等腰三角形.
的角平分线总垂直于x轴,求证:直线AB与两坐标轴围成的三角形一定是等腰三角形.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥PABCD中,底面ABCD是矩形,PA⊥平面ABCD,AD=1,PA=AB=![]() ,点E是棱PB的中点.
,点E是棱PB的中点.

(1)求异面直线EC与PD所成角的余弦值;
(2)求二面角B-EC-D的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com