
【题目】设函数![]() (
(![]() ,且
,且![]() ),
),![]() ,(其中
,(其中![]() 为
为![]() 的导函数).
的导函数).
(1)当![]() 时,求
时,求![]() 的极大值点;
的极大值点;
(2)讨论![]() 的零点个数.
的零点个数.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】试题分析:(1)令![]() 求出
求出![]() 的极值点,判断
的极值点,判断![]() 的符号变化即可得出答案;
的符号变化即可得出答案;
(2)对a和x进行讨论,利用零点的存在性定理,结合函数的图象判断零点的个数.
试题解析:
(1)![]() ,
,
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,故
,故![]() 的极大值点为
的极大值点为![]() ;
;
(2)(i)先考虑![]() 时,
时, ![]() 的零点个数,当
的零点个数,当![]() 时,
时, ![]() 为单减函数,
为单减函数,
![]() ;
; ![]() ,由零点存在性定理知
,由零点存在性定理知![]() 有一个零点;
有一个零点;
当![]() 时,由
时,由![]() 得
得
![]() ,令
,令![]() ,则
,则![]() .
.
由![]() 得,
得, ![]() ,当
,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
故![]() ,
, ![]() ,且
,且![]() 总成立,故
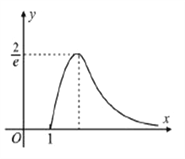
总成立,故![]() 的图像如下图,
的图像如下图,
由数形结合知,
②若![]() 即
即![]() 时,当
时,当![]() 时,
时, ![]() 无零点,故
无零点,故![]() 时,
时, ![]() 有一个零点;
有一个零点;
②若![]() 即
即![]() 时,当
时,当![]() 时,
时, ![]() 有一个零点,故
有一个零点,故![]() 时,
时, ![]() 有
有![]() 个零点;
个零点;
③若![]() 即
即![]() ,当
,当![]() 时,
时, ![]() 有
有![]() 个零点,故
个零点,故![]() 时,
时, ![]() 有
有![]() 个零点.
个零点.
(ii)再考虑![]() 的情形,若
的情形,若![]() ,则
,则![]() ,同上可知,
,同上可知,
当![]() 即
即![]() 时,
时, ![]() 有一个零点;
有一个零点;
当![]() 即
即![]() 时,
时, ![]() 有
有![]() 个零点;
个零点;
当![]() 即
即![]() 时,
时, ![]() 有
有![]() 个零点.
个零点.
综合上述,
①当![]() 或
或![]() 时,
时, ![]() 有一个零点;
有一个零点;
②当![]() 或
或![]() 时,
时, ![]() 有
有![]() 个零点;
个零点;
③当![]() 或
或![]() 时,
时, ![]() 有
有![]() 个零点.
个零点.


科目:高中数学 来源: 题型:
【题目】某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿场售价与上市时间的关系如图一的一条折线表示;西红柿的种植成本与上市时间的关系如图二的抛物线段表示.
(1)写出图一表示的市场售价与时间的函数关系式p=f(t);写出图二表示的种植成本与时间的函数关系式Q=g(t);
(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?(注:市场售价各种植成本的单位:元/102㎏,时间单位:天)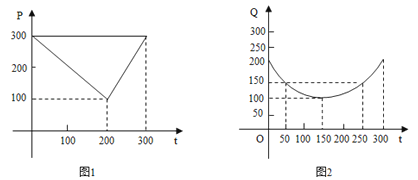
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,M、N、K分别是正方体ABCD﹣A1B1C1D1的棱AB,CD,C1D1的中点.求证:
(1)AN∥平面A1MK;
(2)MK⊥平面A1B1C.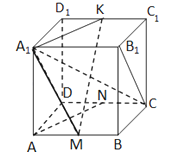
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】酒后违法驾驶机动车危害巨大,假设驾驶人员血液中的酒精含量为![]() (简称血酒含量,单位是毫克/100毫升),当
(简称血酒含量,单位是毫克/100毫升),当![]() 时,为酒后驾车;当
时,为酒后驾车;当![]() 时,为醉酒驾车.如图为某市交管部分在一次夜间行动中依法查出的
时,为醉酒驾车.如图为某市交管部分在一次夜间行动中依法查出的![]() 名饮酒后违法驾驶机动车者抽血检测后所得频率分布直方图(其中
名饮酒后违法驾驶机动车者抽血检测后所得频率分布直方图(其中![]() 人数包含
人数包含![]() ).
).
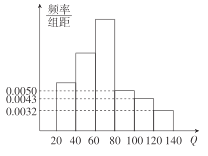
(Ⅰ)求查获的醉酒驾车的人数;
(Ⅱ)从违法驾车的![]() 人中按酒后驾车和醉酒驾车利用分层抽样抽取
人中按酒后驾车和醉酒驾车利用分层抽样抽取![]() 人做样本进行研究,再从抽取的
人做样本进行研究,再从抽取的![]() 人中任取
人中任取![]() 人,求
人,求![]() 人中含有醉酒驾车人数
人中含有醉酒驾车人数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知动点![]() 到直线
到直线![]() 的距离是它到点
的距离是它到点![]() 的距离的
的距离的![]() 倍.
倍.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设轨迹![]() 上一动点
上一动点![]() 满足:
满足: ![]() ,其中
,其中![]() 是轨迹
是轨迹![]() 上的点,且直线
上的点,且直线![]() 与
与![]() 的斜率之积为
的斜率之积为![]() ,若
,若![]() 为一动点,
为一动点, 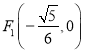 ,
, 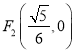 为两定点,求
为两定点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() ,定义
,定义![]() 为数列
为数列![]() 的一阶差分数列,其中
的一阶差分数列,其中![]() ,(
,( ![]() ),设
),设![]()
(1)若![]() ,求证:
,求证: ![]() 是等比数列,并求出
是等比数列,并求出![]() 的通项公式;
的通项公式;
(2)若![]() ,又数列
,又数列![]() 满足:
满足: ![]() :
:
①求数列![]() 的前
的前![]() 和
和![]() ;
;
②求证:数列![]() 中的任意一项总可以表示成该数列中其他两项之积.
中的任意一项总可以表示成该数列中其他两项之积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠DAB=90°,∠ADC=135°,AB=5,CD=2![]() , AD=2,求四边形绕AD旋转一周所围成几何体的表面积及体积.
, AD=2,求四边形绕AD旋转一周所围成几何体的表面积及体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系![]() 中,过椭圆
中,过椭圆![]() :
: ![]() (
(![]() )焦点的直线
)焦点的直线![]() 交
交![]() 于
于![]() 两点,
两点, ![]() 为
为![]() 的中点,且
的中点,且![]() 的斜率为9.
的斜率为9.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)![]() 是
是![]() 的左、右顶点,
的左、右顶点, ![]() 是
是![]() 上的两点,若
上的两点,若![]() ,求四边形
,求四边形![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com