
【题目】如图,三棱柱![]() 中,
中, ![]() ,
, ![]() ,
, ![]() .
.
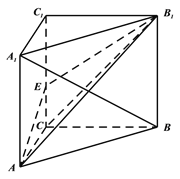
(Ⅰ)证明: ![]() ;
;
(Ⅱ)若![]() ,在棱
,在棱![]() 上是否存在点
上是否存在点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ,若存在,求
,若存在,求![]() 的长,若不存在,说明理由.
的长,若不存在,说明理由.
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】某单位计划在一水库建一座至多安装3台发电机的水电站,过去50年的水文资料显示,水库年入流量![]() (年入流量:一年内上游来水与库区降水之和,单位:亿立方米)都在40以上,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
(年入流量:一年内上游来水与库区降水之和,单位:亿立方米)都在40以上,不足80的年份有10年,不低于80且不超过120的年份有35年,超过120的年份有5年,将年入流量在以上三段的频率作为相应段的概率,假设各年的年入流量相互独立.
(1)求未来3年中,设![]() 表示流量超过120的年数,求
表示流量超过120的年数,求![]() 的分布列及期望;
的分布列及期望;
(2)水电站希望安装的发电机尽可能运行,但每年发电机最多可运行台数受年入流量![]() 限制,并有如下关系:
限制,并有如下关系:
年入流量 |
|
|
|
发电机最多可运行台数 | 1 | 2 | 3 |
若某台发电机运行,则该台年利润为5000万元,若某台发电机未运行,则该台年亏损800万元,欲使水电站年总利润的均值达到最大,应安装发电机多少台?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市垃圾处理站每月的垃圾处理量最少为400吨,最多为600吨,月处理成本![]() (元)与月垃圾处理量
(元)与月垃圾处理量![]() (吨)之间的函数关系可近似地表示为
(吨)之间的函数关系可近似地表示为![]() ,且每处理一吨垃圾得到可利用的资源值为100元.
,且每处理一吨垃圾得到可利用的资源值为100元.
(1)该站每月垃圾处理量为多少吨时,才能使每吨垃圾的平均处理成本最低?
(2)该站每月能否获利?如果获利,求出最大利润;如果不获利,则需要市财政补贴,至少补贴多少元才能使该站不亏损?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若![]() ,证明:函数
,证明:函数![]() 在
在![]() 上单调递减;
上单调递减;
(Ⅱ)是否存在实数![]() ,使得函数
,使得函数![]() 在
在![]() 内存在两个极值点?若存在,求实数
内存在两个极值点?若存在,求实数![]() 的取值范围;若不存在,请说明理由. (参考数据:
的取值范围;若不存在,请说明理由. (参考数据: ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其中
,其中![]() 为常数,
为常数, ![]() 为自然对数的底数.
为自然对数的底数.
(1)若![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,求
,求![]() 的值;
的值;
(2)当![]() 时,判断方程
时,判断方程![]() 是否有实根?若无实根请说明理由,若有实根请给出根的个数.
是否有实根?若无实根请说明理由,若有实根请给出根的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】心理学家分析发现视觉和空间能力与性别有关,某数学兴趣小组为了验证这个结论,从兴趣小组中按分层抽样的方法抽取50名同学(男30女20),给所有同学几何题和代数题各一题,让各位同学自由选择一道题进行解答.选题情况如下表:(单位:人)
几何题 | 代数题 | 总计 | |
男同学 | 22 | 8 | 30 |
女同学 | 8 | 12 | 20 |
总计 | 30 | 20 | 50 |
(Ⅰ)能否据此判断有97.5%的把握认为视觉和空军能力与性别有关?
(Ⅱ)经过多次测试后,甲每次解答一道几何题所用的时间在5—7分钟,乙每次解答一道几何题所用的时间在6—8分钟,现甲、乙各解同一道几何题,求乙比甲先解答完的概率.
(Ⅲ)现从选择做几何题的8名女生中任意抽取两人对她们的答题情况进行全程研究,记甲、乙两女生被抽到的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附表及公式
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
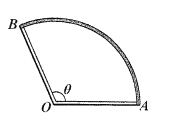
【题目】园林管理处拟在公园某区域规划建设一半径为![]() 米,圆心角为
米,圆心角为![]() (弧度)的扇形观景水池,其中
(弧度)的扇形观景水池,其中![]() ,
, ![]() 为扇形
为扇形![]() 的圆心,同时紧贴水池周边(即:
的圆心,同时紧贴水池周边(即: ![]() 和
和![]() 所对的圆弧)建设一圈理想的无宽度步道.要求总预算费用不超过24万元,水池造价为每平方米400元,步道造价为每米1000元.
所对的圆弧)建设一圈理想的无宽度步道.要求总预算费用不超过24万元,水池造价为每平方米400元,步道造价为每米1000元.
(1)若总费用恰好为24万元,则当![]() 和
和![]() 分别为多少时,可使得水池面积最大,并求出最大面积;
分别为多少时,可使得水池面积最大,并求出最大面积;
(2)若要求步道长为105米,则可设计出的水池最大面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2-a)lnx+![]() +2ax.
+2ax.
(1)当a<0时,讨论f(x)的单调性;
(2)若对任意的a∈(-3,-2),x1,x2∈[1,3],恒有(m+ln 3)a-2ln 3>|f(x1)-f(x2)|成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com