
【题目】有甲、乙两个桔柚(球形水果)种植基地,已知所有采摘的桔柚的直径都在![]() 范围内(单位:毫米,以下同),按规定直径在
范围内(单位:毫米,以下同),按规定直径在![]() 内为优质品,现从甲、乙两基地所采摘的桔柚中各随机抽取500个,测量这些桔柚的直径,所得数据整理如下:
内为优质品,现从甲、乙两基地所采摘的桔柚中各随机抽取500个,测量这些桔柚的直径,所得数据整理如下:

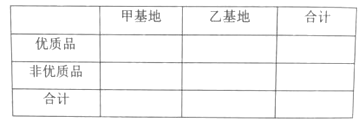
(1)根据以上统计数据完成下面![]() 列联表,并回答是否有
列联表,并回答是否有![]() 以上的把握认为“桔柚直径与所在基地有关”?
以上的把握认为“桔柚直径与所在基地有关”?
(2)求优质品率较高的基地的500个桔柚直径的样本平均数![]() (同一组数据用该区间的中点值作代表);
(同一组数据用该区间的中点值作代表);
(3)记甲基地直径在![]() 范围内的五个桔柚分别为
范围内的五个桔柚分别为![]() ,现从中任取二个,求含桔柚
,现从中任取二个,求含桔柚![]() 的概率.
的概率.
附: 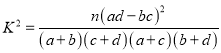 ,
, ![]() .
.

【答案】(1) 有95%的把握认为:“桔柚直径与所在基地有关;(2)80;(3) ![]() .
.
【解析】试题分析:(1)先写出列联表,然后根据公式代入数值求解对照表格下结论即可;(2)平均数计算公式为: ![]() ;(3)根据古典概型的概率求法将基本时间一一列出,再得出符合条件的基本事件,求比值即可得概率
;(3)根据古典概型的概率求法将基本时间一一列出,再得出符合条件的基本事件,求比值即可得概率
解析:
(Ⅰ)由以上统计数据填写![]() 列联表如下:
列联表如下:
甲基地 | 乙基地 | 合计 | |
优质品 | 420 | 390 | 810 |
非优质品 | 80 | 110 | 190 |
合计 | 500 | 500 | 1000 |
![]()
所以,有95%的把握认为:“桔柚直径与所在基地有关”.
(Ⅱ)甲基地桔柚的优质品率为![]() ,乙基地桔柚的优质品率为
,乙基地桔柚的优质品率为![]() ,
,
所以,甲基地桔柚的优质品率较高,
甲基地的500个桔柚直径的样本平均数![]()
![]()
(Ⅲ)依题意:记“从甲基地直径在![]() 的五个桔柚A,B,C,D,E中任取二个,含桔柚A”为事件N.
的五个桔柚A,B,C,D,E中任取二个,含桔柚A”为事件N.
实验包含的所有基本事件:(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),
(B,E),(C, D),(C,E),(D,E)共10种.
事件N包含的结果有:(A, B),(A, C),(A,D),(A,E)共4种.
所求事件的概率为: ![]()


科目:高中数学 来源: 题型:
【题目】如图,底面半径为![]() ,母线长为
,母线长为![]() 的圆柱的轴截面是四边形
的圆柱的轴截面是四边形![]() ,线段
,线段![]() 上的两动点
上的两动点![]() ,
, ![]() 满足
满足![]() .点
.点![]() 在底面圆
在底面圆![]() 上,且
上,且![]() ,
, ![]() 为线段
为线段![]() 的中点.
的中点.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)四棱锥![]() 的体积是否为定值,若是,请求出该定值;若不是,请说明理由.
的体积是否为定值,若是,请求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】公元263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形的面积可无限接近圆的面积,并创立了“割圆术”,利用“割圆术”,刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”,利用刘徽的“割圆术”思想设计的一个程序框图,则输出的值为( )
(参考数据: ![]() )
)
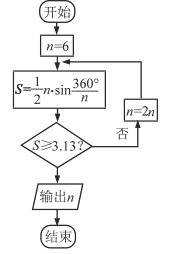
A. 12 B. 24 C. 48 D. 96
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() 的焦点为
的焦点为![]() ,过点
,过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() (
(![]() 位于第一象限)两点.
位于第一象限)两点.
(1)若直线![]() 的斜率为
的斜率为![]() ,过点
,过点![]() 分别作直线
分别作直线![]() 的垂线,垂足分别为
的垂线,垂足分别为![]() ,求四边形
,求四边形![]() 的面积;
的面积;
(2)若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司为了准确把握市场,做好产品计划,特对某产品做了市场调查:先销售该产品50天,统计发现每天的销售量![]() 分布在
分布在![]() 内,且销售量
内,且销售量![]() 的分布频率满足:
的分布频率满足: 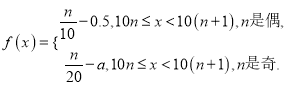
(1)求![]() 的值并估计销售量的平均数;
的值并估计销售量的平均数;
(2)若销售量大于等于80,则称该日畅销,其余为滞销.在畅销日中用分层抽样的方法随机抽取6天,再从这6天中随机抽取3天进行统计,求这3天不都来自同一组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,点
中,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,以
为极点,以![]() 轴的非负半轴为极轴,选择相同的单位长度建立极坐标系,圆
轴的非负半轴为极轴,选择相同的单位长度建立极坐标系,圆![]() 极坐标方程为
极坐标方程为![]() .
.
(Ⅰ)当![]() 时,求直线
时,求直线![]() 的普通方程和圆
的普通方程和圆![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)直线![]() 与圆
与圆![]() 的交点为
的交点为![]() 、
、![]() ,证明:
,证明:![]() 是与
是与![]() 无关的定值.
无关的定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com