
【题目】已知函数![]() .
.
(1)当![]() 时,判断函数
时,判断函数![]() 的单调性;
的单调性;
(2)若![]() 恒成立,求a的取值范围;
恒成立,求a的取值范围;
(3)已知![]() ,证明
,证明![]() .
.
【答案】(1)![]() 在区间
在区间![]() 单调递增,
单调递增,![]() 单调递减 (2)
单调递减 (2)![]() (3)证明见解析
(3)证明见解析
【解析】
(1)当![]() 时,
时,![]() ,分析出
,分析出![]() 的正负,从而得
的正负,从而得![]() 的单调区间;
的单调区间;
(2)由已知分离变量得![]() 恒成立.设
恒成立.设![]() ,则
,则![]() ,对
,对![]() 求导,分析出
求导,分析出![]() 的正负,从而得
的正负,从而得![]() 的单调区间和最值,可得a的取值范围;
的单调区间和最值,可得a的取值范围;
(3)欲证![]() ,两边取对数,转化为
,两边取对数,转化为![]() ,由(2)可知
,由(2)可知![]() 的单调性,可得证.
的单调性,可得证.
由题意可知,函数![]() 的定义域为:
的定义域为:![]() 且
且![]() ,
,
(1)当![]() 时,
时,![]() ,
,
若![]() ,则
,则![]() ;若
;若![]() ,则
,则![]() ,
,
所以函数![]() 在区间
在区间![]() 单调递增,
单调递增,![]() 单调递减.
单调递减.
(2)若![]() 恒成立,则
恒成立,则![]() 恒成立.
恒成立.
又因为![]() ,所以分离变量得
,所以分离变量得![]() 恒成立.
恒成立.
设![]() ,则
,则![]() ,所以
,所以![]() .
.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
即函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
当![]() 时,函数
时,函数![]() 取最大值,
取最大值,![]() ,所以
,所以![]() .
.
(3)欲证![]() ,两边取对数,可得
,两边取对数,可得![]() ,
,
由(2)可知![]() 在
在![]() 上单调递增,且
上单调递增,且![]() 所以
所以![]() ,命题得证.
,命题得证.


科目:高中数学 来源: 题型:
【题目】某种大型医疗检查机器生产商,对一次性购买2台机器的客户,推出两种超过质保期后两年内的延保维修优惠方案:方案一:交纳延保金7000元,在延保的两年内可免费维修2次,超过2次每次收取维修费2000元;方案二:交纳延保金10000元,在延保的两年内可免费维修4次,超过4次每次收取维修费1000元.某医院准备一次性购买2台这种机器。现需决策在购买机器时应购买哪种延保方案,为此搜集并整理了50台这种机器超过质保期后延保两年内维修的次数,得下表:
维修次数 | 0 | 1 | 2 | 3 |
台数 | 5 | 10 | 20 | 15 |
以这50台机器维修次数的频率代替1台机器维修次数发生的概率,记X表示这2台机器超过质保期后延保的两年内共需维修的次数。
(1)求X的分布列;
(2)以所需延保金及维修费用的期望值为决策依据,医院选择哪种延保方案更合算?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是曲线
是曲线![]() 上两点,
上两点,![]() 两点的横坐标之和为4,直线
两点的横坐标之和为4,直线![]() 的斜率为2.
的斜率为2.
(1)求曲线![]() 的方程;
的方程;
(2)设![]() 是曲线
是曲线![]() 上一点,曲线
上一点,曲线![]() 在
在![]() 点处的切线与直线
点处的切线与直线![]() 平行,且
平行,且![]() ,试求三角形
,试求三角形![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=|2x﹣3|+|x+2|
(1)求不等式f(x)≤5的解集;
(2)若关于x的不等式f(x)≤a﹣|x|在区间[﹣1,2]上恒成立,求实数a的取值范围
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,直线l的参数方程为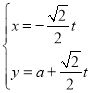 (t为参数,a∈R),以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ
(t为参数,a∈R),以O为极点,x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ
(1)求直线l的普通方程及曲线C的直角坐标方程;
(2)若直线l过点P(1,1)且与曲线C交于AB两点,求|PA|+|PB|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴建立极坐标系,已知点
轴的正半轴为极轴建立极坐标系,已知点![]() 的直角坐标为
的直角坐标为![]() ,若直线
,若直线![]() 的极坐标方程为
的极坐标方程为![]() 曲线
曲线![]() 的参数方程是
的参数方程是![]() (
(![]() 为参数).
为参数).
(1)求直线![]() 和曲线
和曲线![]() 的普通方程;
的普通方程;
(2)设直线![]() 和曲线
和曲线![]() 交于
交于![]() 两点,求
两点,求![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知离心率为![]() 的椭圆
的椭圆![]()
![]() 的左顶点为A,且椭圆E经过
的左顶点为A,且椭圆E经过![]() 与坐标轴不垂直的直线l与椭圆E交于C,D两点,且直线AC和直线AD的斜率之积为
与坐标轴不垂直的直线l与椭圆E交于C,D两点,且直线AC和直线AD的斜率之积为![]() .
.
(I)求椭圆E的标准方程;
(Ⅱ)求证:直线l过定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com