
【题目】已知![]() .
.
(1)若![]() 有两个零点,求
有两个零点,求![]() 的范围;
的范围;
(2)若![]() 有两个极值点,求
有两个极值点,求![]() 的范围;
的范围;
(3)在(2)的条件下,若![]() 的两个极值点为
的两个极值点为![]()
![]() ,求证:
,求证: ![]() .
.
【答案】(1) ![]() (2)
(2) ![]() (3) 见解析
(3) 见解析
【解析】试题分析:(1)由题意函数![]() 必有极值点,且极大值大于零,列对应不等式,解得
必有极值点,且极大值大于零,列对应不等式,解得![]() 的范围;(2)先求导数,得
的范围;(2)先求导数,得![]() 有两个改变
有两个改变![]() 符号的零点,即导函数
符号的零点,即导函数![]() 必有极值点,且极大值大于零,列对应不等式,解得
必有极值点,且极大值大于零,列对应不等式,解得![]() 的范围;(3)由(2)
的范围;(3)由(2)![]() 再利用极值点条件构造函数
再利用极值点条件构造函数![]() ,最后利用导数研究函数单调性,根据最值证不等式
,最后利用导数研究函数单调性,根据最值证不等式
试题解析:方法一:
(1)![]()
![]() 有两个零点,
有两个零点, ![]() 有两个零点
有两个零点
![]()
![]() 时
时![]() 在
在![]() 上单调,最多有一个零点,不合题意
上单调,最多有一个零点,不合题意
![]() 在
在![]() 上↑,在
上↑,在![]() 上↓
上↓
![]()
又![]() 时,
时, ![]()
![]() 必有两个零点
必有两个零点
![]()
(2)![]() 有两个改变
有两个改变![]() 符号的零点
符号的零点
设![]() 则
则![]()
![]() 时,
时, ![]() 恒成立,
恒成立, ![]() 在
在![]() 上单调,最多有一个零点,不合题意
上单调,最多有一个零点,不合题意
![]() 由
由![]() 得:
得: ![]() ,
,
![]() 在
在![]() 上↑,在
上↑,在![]() 上↓
上↓
![]() ,即
,即![]()
又![]()
![]() 在
在![]() 各有一个零点
各有一个零点
![]()
(3)由(2),结合h(1)=1-2a>0,知![]()
![]()
设![]()
![]() 在
在![]() 上↓,
上↓,![]()
![]()
方法二:分离参数法
(1)![]() ,两图象有两交点
,两图象有两交点
令![]()
当![]()
当![]() ,
, ![]()
结合图像, ![]() 。
。
(2)![]() 有两个改变
有两个改变![]() 符号的零点
符号的零点
等价于![]() 对应的两函数的图像有两交点
对应的两函数的图像有两交点
令![]()
当![]()
当![]()
结合图象, ![]()
(3)由(2)![]()
![]()


科目:高中数学 来源: 题型:
【题目】用![]() ,
,![]() ,
,![]() 表示空间中三条不同的直线,
表示空间中三条不同的直线,![]() 表示平面, 给出下列命题:
表示平面, 给出下列命题:
① 若![]() ,
,![]() , 则
, 则![]() ∥
∥![]() ; ② 若
; ② 若![]() ∥
∥![]() ,
,![]() ∥
∥![]() , 则
, 则![]() ∥
∥![]() ;
;
③ 若![]() ∥
∥![]() ,
,![]() ∥
∥![]() , 则
, 则![]() ∥
∥![]() ; ④ 若
; ④ 若![]()
![]()
![]() ,
,![]()
![]()
![]() , 则
, 则![]() ∥
∥![]() .
.
其中真命题的序号是( )
A. ①② B. ②③ C. ①④ D. ②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)满足:对任意![]() 都有
都有![]() ,且当x>0时,
,且当x>0时,![]() .
.
(1)求![]() 的值,并证明
的值,并证明![]() 为奇函数;
为奇函数;
(2)判断函数![]() 的单调性,并证明;
的单调性,并证明;
(3)若![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我校为了让高一学生更有效率地利用周六的时间,在高一新生第一次摸底考试后采取周六到校自主学习,同时由班主任老师值班,家长轮流值班.一个月后进行了第一次月考,高一数学教研组通过系统抽样抽取了![]() 名学生,并统计了他们这两次数学考试的优良人数和非优良人数,其中部分统计数据如下:
名学生,并统计了他们这两次数学考试的优良人数和非优良人数,其中部分统计数据如下:

(1)请画出这次调查得到的![]() 列联表;并判定能否在犯错误概率不超过
列联表;并判定能否在犯错误概率不超过![]() 的前提下认为周六到校自习对提高学生成绩有效?
的前提下认为周六到校自习对提高学生成绩有效?
(2)从这组学生摸底考试中数学优良成绩中和第一次月考的数学非优良成绩中,按分层抽样随机抽取![]() 个成绩,再从这
个成绩,再从这![]() 个成绩中随机抽取
个成绩中随机抽取![]() 个,求这
个,求这![]() 个成绩来自同一次考试的概率.
个成绩来自同一次考试的概率.
下面是临界值表供参考:

(参考公式:  ,其中
,其中![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 过点
过点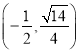 ,且离心率为
,且离心率为![]() .过点
.过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)若点![]() 为椭圆
为椭圆![]() 的右顶点,探究:
的右顶点,探究: ![]() 是否为定值,若是,求出该定值,若不是,请说明理由.(其中,
是否为定值,若是,求出该定值,若不是,请说明理由.(其中, ![]() ,
, ![]() 分别是直线
分别是直线![]() 、
、![]() 的斜率)
的斜率)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com