Question

在正方体ABCD-A₁B₁C₁D₁中，E、F分别是BB₁、CD的中点．
（1）求证：平面AED⊥平面A₁FD₁；
（2）在AE上求一点M，使得A₁M⊥平面ADE．

Answer 1

分析：（1）建立如图所示的空间直角坐标系D-xyz，不妨设正方体的棱长为2，设平面AED的法向量为

n1

=（x₁，y₁，z₁），
利用

n1

•

DA

=0，

n1

•

DE

=0，得

n1

=（0，1，-2），同理可得平面A₁FD₁的法向量

n2

=（0，2，1）．
通过

n1

•

n2

=0，证明平面AED⊥平面A₁FD₁．
（2）由于点M在直线AE上，设

AM

=（0，2λ，λ）．

A1M

=（0，2λ，λ-2），利用AD⊥A₁M，

A1M

•

AE

=0，推出5λ-2=0，
解得λ=

2

5

．故当A=

2

5

A时，A₁M⊥平面ADE点M在直线AE上，

解答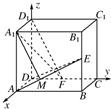：证明：（1）建立如图所示的空间直角坐标系D-xyz，
不妨设正方体的棱长为2，则A（2，0，0），E（2，2，1），
F（0，1，0），A₁（2，0，2），D₁（0，0，2），
设平面AED的法向量为

n1

=（x₁，y₁，z₁），
则

n1

•

DA

=（x₁，y₁，z₁）•（2，0，0）=0，

n1

•

DE

=（x₁，y₁，z₁）•（2，2，1）=0，
∴2x₁=0，2x₁+2y₁+z₁=0．
令y₁=1，得

n1

=（0，1，-2），
同理可得平面A₁FD₁的法向量

n2

=（0，2，1）．
∵

n1

•

n2

=0，∴

n1

⊥

n2

，
∴平面AED⊥平面A₁FD₁．
（2）由于点M在直线AE上，
设

AM

=λ（0，2，1）=（0，2λ，λ）．
可得M（2，2λ，λ），∴

A1M

=（0，2λ，λ-2），
∵AD⊥A₁M，∴要使A₁M⊥平面ADE，
只需A₁M⊥AE，
∴

A1M

•

AE

=（0，2λ，λ-2）•（0，2，1）=5λ-2=0，
解得λ=

2

5

．故当A=

2

5

A时，A₁M⊥平面ADE

点评：本题是中档题，考查平面与平面的垂直，注意向量的数量积的应用，直线与平面的垂直，考查计算能力，常考题型．