
| x2 |
| a2 |
| y2 |
| b2 |
| a(a2-b2) |
| a2+b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| a(a2-b2) |
| a2+b2 |
|
| b2 |
| k2 |
|
| 2b |
| k |
| b2 |
| k2 |
| 2b |
| k |
|
| 2m |
| 1 |
| |AF| |
| 1 |
| |BF| |
| 2a |
| b2 |


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
| 4 |
| 5 |
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 2 |
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |

| k |
| 2 |
| k |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| y2 |
| a |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源:2011年5月广东省梅州市中学高三(下)月考数学试卷(理科)(解析版) 题型:填空题
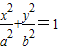 (a>b>0)上的一点,F1、F2是左、右两个焦点,若△PF1F2的内切圆的半径为
(a>b>0)上的一点,F1、F2是左、右两个焦点,若△PF1F2的内切圆的半径为 ,则此椭圆的离心率
,则此椭圆的离心率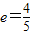 ;
;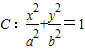 (a>b>0)上的任意一动点M,引圆O:x2+y2=b2的两条切线MA、MB,切点分别为A、B,若
(a>b>0)上的任意一动点M,引圆O:x2+y2=b2的两条切线MA、MB,切点分别为A、B,若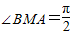 ,则椭圆的离心率e的取值范围为
,则椭圆的离心率e的取值范围为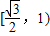 ;
;查看答案和解析>>
科目:高中数学 来源:2013年湖南省怀化市高考数学二模试卷(理科)(解析版) 题型:选择题
 的椭圆,使两端点A、B恰好重合于椭圆的一个短轴端点,如图2;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在x轴上,已知此时点A的坐标为(0,1),如图3,在图形变化过程中,图1中线段AM的长度对应于图3中的椭圆弧ADM的长度.图3中直线AM与直线y=-2交于点N(n,-2),则与实数m对应的实数就是n,记作f(m)=n,
的椭圆,使两端点A、B恰好重合于椭圆的一个短轴端点,如图2;再将这个椭圆放在平面直角坐标系中,使其中心在坐标原点,长轴在x轴上,已知此时点A的坐标为(0,1),如图3,在图形变化过程中,图1中线段AM的长度对应于图3中的椭圆弧ADM的长度.图3中直线AM与直线y=-2交于点N(n,-2),则与实数m对应的实数就是n,记作f(m)=n,
 ;②函数f(m)是奇函数;③函数f(m)在(0,k)上单调递增;④函数f(m)的图象关于点
;②函数f(m)是奇函数;③函数f(m)在(0,k)上单调递增;④函数f(m)的图象关于点 对称;⑤函数
对称;⑤函数 时AM过椭圆的右焦点.其中所有的真命题是( )
时AM过椭圆的右焦点.其中所有的真命题是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com