
【题目】函数 ![]() ,则下列结论错误的是( )
,则下列结论错误的是( )
A.f(x)是偶函数
B.方程f(f(x))=x的解为x=1
C.f(x)是周期函数
D.方程f(f(x))=f(x)的解为x=1
【答案】D
【解析】解:∵函数 ![]() ,
,
当x为有理数时,﹣x必为有理数,此时f(﹣x)=f(x)=1;当x为无理数时,﹣x必为无理数,此时f(﹣x)=f(x)=0.故Af(x)是偶函数正确;
若为有理数,则方程f(f(x))=f(1)=1,此时x=1;若为无理数,则方程f(f(x))=f(0)=1,此时无满足条件的x;故B方程f(f(x))=x的解为x=1正确;
对于任意的有理数T,当x为有理数时,x+T必为有理数,此时f(x+T)=f(x)=1;当x为无理数时,x+T必为无理数,此时f(x+T)=f(x)=0;即函数是周期为任意非0有理数的周期函数,故Cf(x)是周期函数正确;
若为有理数,则方程f(f(x))=f(1)=1=f(x)恒成立;若为无理数,则方程f(f(x))=f(0)=1≠f(x),此时无满足条件的x;故方程f(f(x))=f(x)的解为任意有理数,故D错误;
故答案选:D
【考点精析】关于本题考查的命题的真假判断与应用和函数的零点,需要了解两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系;函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点才能得出正确答案.


科目:高中数学 来源: 题型:
【题目】在四棱锥P﹣ABCD中,AB⊥AD,CD⊥AD,PA⊥平面ABCD,PA=AD=CD=2AB=2,M为PC的中点. (Ⅰ)求证:BM∥平面PAD;
(Ⅱ)平面PAD内是否存在一点N,使MN⊥平面PBD?若存在,确定点N的位置;若不存在,请说明理由.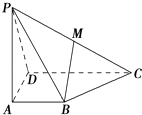
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知底面为边长为2的正方形,侧棱长为1的直四棱柱ABCD﹣A1B1C1D1中,P是面A1B1C1D1上的动点.给出以下四个结论中,正确的个数是( ) ①与点D距离为 ![]() 的点P形成一条曲线,则该曲线的长度是
的点P形成一条曲线,则该曲线的长度是 ![]() ;
;
②若DP∥面ACB1 , 则DP与面ACC1A1所成角的正切值取值范围是 ![]() ;
;
③若 ![]() ,则DP在该四棱柱六个面上的正投影长度之和的最大值为
,则DP在该四棱柱六个面上的正投影长度之和的最大值为 ![]() .
.
A.0
B.1
C.2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为抛物线C:y2=4x的焦点,点P是准线l上的动点,直线PF交抛物线C于A,B两点,若点P的纵坐标为m(m≠0),点D为准线l与x轴的交点. (Ⅰ)求直线PF的方程;
(Ⅱ)求△DAB的面积S范围;
(Ⅲ)设 ![]() ,
, ![]() ,求证λ+μ为定值.
,求证λ+μ为定值.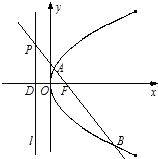
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|x2﹣6x+5<0},B={x| ![]() <2x﹣4<16},C={x|﹣a<x≤a+3}
<2x﹣4<16},C={x|﹣a<x≤a+3}
(1)求A∪B和(RA)∩B
(2)若A∪C=A,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网店经营的一种商品进行进价是每件10元,根据一周的销售数据得出周销售量 ![]() (件)与单价
(件)与单价 ![]() (元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
(元)之间的关系如下图所示,该网店与这种商品有关的周开支均为25元.
(1)根据周销售量图写出 ![]() (件)与单价
(件)与单价 ![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)写出利润 ![]() (元)与单价
(元)与单价 ![]() (元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
(元)之间的函数关系式;当该商品的销售价格为多少元时,周利润最大?并求出最大周利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com