
【题目】已知函数![]() (a
(a![]() R),其中e为自然对数的底数.
R),其中e为自然对数的底数.
(1)若![]() ,求函数
,求函数![]() 的单调减区间;
的单调减区间;
(2)若函数![]() 的定义域为R,且
的定义域为R,且![]() ,求a的取值范围;
,求a的取值范围;
(3)证明:对任意![]() ,曲线
,曲线![]() 上有且仅有三个不同的点,在这三点处的切线经过坐标原点.
上有且仅有三个不同的点,在这三点处的切线经过坐标原点.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)当![]() 时,
时,![]() ,定义域为R.求出
,定义域为R.求出![]() ,令
,令![]() ,即得
,即得![]() 的单调减区间;
的单调减区间;
(2)由函数![]() 的定义域为R,得
的定义域为R,得![]() 恒成立,故
恒成立,故![]() ,得
,得![]() .分
.分![]() 三种情况讨论,即得a的取值范围;
三种情况讨论,即得a的取值范围;
(3)设切点为![]() ,求出
,求出![]() ,写出切线方程.把点
,写出切线方程.把点![]() 代入,化简得
代入,化简得![]() .令
.令![]() ,求出
,求出![]() ,判断
,判断![]() 的单调性,结合零点存在定理,即可证明.
的单调性,结合零点存在定理,即可证明.
(1)当![]() 时,
时,![]() ,定义域为R..
,定义域为R..
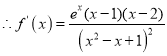 .
.
令![]() ,得
,得![]() ,
,
![]() 函数
函数![]() 的单调减区间为
的单调减区间为![]() .
.
(2)由函数![]() 的定义域为R,得
的定义域为R,得![]() 恒成立,
恒成立,
![]() .
.
由![]() ,得
,得 .
.
当![]() 时,
时,![]() ,不符合题意.
,不符合题意.
当![]() 时,
时,![]() 当
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,![]() ,不符题意.
,不符题意.
当![]() 时,
时,![]() 当
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,![]() ,满足题意.
,满足题意.
综上,a的取值范围为![]() .
.
(3)证明:设切点为![]() ,则
,则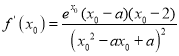 ,
,
![]() 切线方程为
切线方程为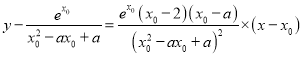 .
.
由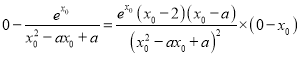 ,化简得
,化简得![]() .
.
设![]() ,则只需证明函数
,则只需证明函数![]() 有且仅有三个不同的零点.
有且仅有三个不同的零点.
由(2)可知![]() 时,函数
时,函数![]() 的定义域为R,
的定义域为R,![]() .
.
![]() 恒成立,
恒成立,
![]() 有两不相等的实数根x1和x2,不妨
有两不相等的实数根x1和x2,不妨![]() .
.
可得下表:
x | (-∞,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
h’(x) | + | 0 | - | 0 | + |
h(x) | 增 | 极大值 | 减 | 极小值 | 增 |
所以函数h(x)最多有三个零点.
![]() ,
,![]() ,
,
![]() .
.
![]() 函数
函数![]() 的图象不间断,
的图象不间断,![]() 函数
函数![]() 在
在![]() 上分别至少有一个零点.
上分别至少有一个零点.
综上所述,函数h(x)有且仅有三个零点,即对任意![]() ,曲线
,曲线![]() 上有且仅有三个不同的点,在这三点处的切线经过坐标原点.
上有且仅有三个不同的点,在这三点处的切线经过坐标原点.


科目:高中数学 来源: 题型:
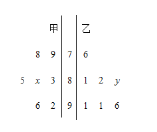
【题目】某中学从甲、乙两个班中各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图所示,其中甲班学生成绩的众数是83,乙班学生成绩的平均数是86,则![]() 的值为( )
的值为( )
A.7B.8C.9D.10
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在长方体ABCD﹣A1B1C1D1中,AA1=2AB=2AD=4,过AA1作平面α使BD⊥α,且平面α∩平面A1B1C1D1=l,M∈l.下面给出了四个命题:这四个命题中,真命题的个数为( )
①l∥AC;
②BM⊥AC;
③l和AD1所成的角为60°;
④线段BM长度的最小值为![]() .
.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小学的期末考试中抽取部分学生的数学成绩,由抽查结果得到如图的频率分布直方图,分数落在区间![]() ,
,![]() ,
,![]() 内的频率之比为
内的频率之比为![]() .
.
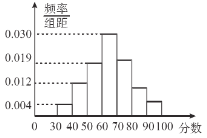
(1)求这些学生的分数落在区间![]() 内的频率;
内的频率;
(2)(ⅰ)若采用分层抽样的方法从分数落在区间![]() ,
,![]() 内抽取4人,求从分数落在区间
内抽取4人,求从分数落在区间![]() ,
,![]() 内各抽取的人数;
内各抽取的人数;
(ⅱ)从上述抽取的4人中再随机抽取2人,求这2人全部来自于区间![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司准备将1000万元资金投人到市环保工程建设中,现有甲,乙两个建设项目选择,若投资甲项目一年后可获得的利润![]() (万元)的概率分布列如表所示:
(万元)的概率分布列如表所示:
| 110 | 120 | 170 |
|
| 0.4 |
|
且![]() 的期望
的期望![]() ;若投资乙项目一年后可获得的利润
;若投资乙项目一年后可获得的利润![]() (万元)与该项目建设材料的成本有关,在生产的过程中,公司将根据成本情况决定是否在第二和第三季度进行产品的价格调整,两次调整相互独立且调整的概率分别为
(万元)与该项目建设材料的成本有关,在生产的过程中,公司将根据成本情况决定是否在第二和第三季度进行产品的价格调整,两次调整相互独立且调整的概率分别为![]() 和
和![]() .若乙项目产品价格一年内调整次数
.若乙项目产品价格一年内调整次数![]() (次数)与
(次数)与![]() 的关系如表所示:
的关系如表所示:
| 0 | 1 | 2 |
| 41.2 | 117.6 | 204.0 |
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 的分布列.
的分布列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,其焦点到准线的距离为2.直线
,其焦点到准线的距离为2.直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,过
两点,过![]() ,
,![]() 分别作抛物线
分别作抛物线![]() 的切线
的切线![]() 与
与![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)若![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线![]() 与椭圆
与椭圆![]() 交于不同的两点
交于不同的两点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,且直线
,且直线![]() 与直线
与直线![]() 的斜率之积为
的斜率之积为![]() .若直线
.若直线![]() 与直线
与直线![]() 交于点
交于点![]() ,与直线
,与直线![]() 交于点
交于点![]() ,且
,且![]() 点为直线
点为直线![]() 上一点.
上一点.
(1)求![]() 的轨迹方程;
的轨迹方程;
(2)若![]() 为椭圆
为椭圆![]() 的上顶点,直线
的上顶点,直线![]() 与
与![]() 轴交点
轴交点![]() ,记
,记![]() 表示面积,求
表示面积,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】孙子定理是中国古代求解一次同余式组的方法,是数论中一个重要定理,最早可见于中国南北朝时期的数学著作《孙子算经》,![]() 年英国来华传教士伟烈亚力将其问题的解法传至欧洲,
年英国来华传教士伟烈亚力将其问题的解法传至欧洲,![]() 年英国数学家马西森指出此法符合
年英国数学家马西森指出此法符合![]() 年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.这个定理讲的是一个关于整除的问题,现有这样一个整除问题:将
年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”.这个定理讲的是一个关于整除的问题,现有这样一个整除问题:将![]() 至
至![]() 这
这![]() 个整数中能被
个整数中能被![]() 除余
除余![]() 且被
且被![]() 除余
除余![]() 的数按由小到大的顺序排成一列构成一数列,则此数列的项数是( )
的数按由小到大的顺序排成一列构成一数列,则此数列的项数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com