Question

设集合A={x|x²+2x-8＞0}，B={x|x²+2kx-3k²+8k-4＜0}，若A∩B≠∅，求k的取值范围．

Answer 1

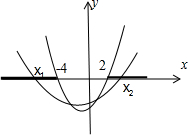
解：易知：A={x|x＜-4或x＞2}，
设f（x）=x²+2kx-3k²+8k-4，判别式△=4k²+12k²-32k+16=16（k-1）²≥0
故方程f（x）=0有二根x₁、x₂，设x₁≤x₂，则B={x|x₁≤x≤x₂}，
要使A∩B≠∅，需 x₁＜-4或x₂＞2，如图，只需f（-4）＜0或f（2）＜0，
解得k＜0或k＞2．
k的取值范围：{x|k＜0或k＞2}．
分析：求出集合A，判断集合B是否存在解，求出集合B，利用A∩B≠∅，直接求出k的取值范围即可．
点评：本题是中档题，考查不等式的解法，交集的求法，注意交集是空集的充要条件，考查计算能力．