
【题目】已知p:指数函数f(x)=(2a-6)x在R上是单调减函数;q:关于x的方程x2-3ax+2a2+1=0的两根均大于3,若p或q为真,p且q为假,求实数a的取值范围.
【答案】(![]() ,3]∪[
,3]∪[![]() ,+∞).
,+∞).
【解析】试题分析:根据指数函数的单调性求出命题p为真命题时a的范围,利用二次方程的实根分布求出命题q为真命题时a的范围;
据复合命题的真假与构成其简单命题真假的关系将“p或q为真,p且q为假”转化为p ,q的真假,列出不等式解得.
试题解析:
p真,则指数函数f(x)=(2a-6)x的底数2a-6满足0<2a-6<1,所以3<a<![]() .
.
q真,令g(x)=x2-3ax+2a2+1,易知其为开口向上的二次函数.因为x2-3ax+2a2+1=0的两根均大于3,所以①Δ=(-3a)2-4(2a2+1)=a2-4>0,a<-2或a>2;②对称轴x=-![]() =
=![]() >3;③g(3)>0,即32-9a+2a2+1=2a2-9a+10>0,所以(a-2)(2a-5)>0.所以a<2或a>
>3;③g(3)>0,即32-9a+2a2+1=2a2-9a+10>0,所以(a-2)(2a-5)>0.所以a<2或a>![]() .
.
由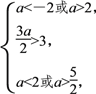 得a>
得a>![]() .
.
p真q假,由3<a<![]() 及a≤
及a≤![]() ,得a∈.
,得a∈.
p假q真,由a≤3或a≥![]() 及a>
及a>![]() ,得
,得![]() <a≤3或a≥
<a≤3或a≥![]() .
.
综上所述,实数a的取值范围为(![]() ,3]∪[
,3]∪[![]() ,+∞).
,+∞).


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:
【题目】如图,海上有![]() 、
、![]() 两个小岛相距
两个小岛相距![]() ,船
,船![]() 将保持观望
将保持观望![]() 岛和
岛和![]() 岛所成的视角为
岛所成的视角为![]() ,现从船
,现从船![]() 上派下一只小艇沿
上派下一只小艇沿![]() 方向驶至
方向驶至![]() 处进行作业,且
处进行作业,且![]() .设
.设![]() .
.

(1)用![]() 分别表示
分别表示![]() 和
和![]() ,并求出
,并求出![]() 的取值范围;
的取值范围;
(2)0晚上小艇在![]() 处发出一道强烈的光线照射
处发出一道强烈的光线照射![]() 岛,
岛,![]() 岛至光线
岛至光线![]() 的距离为
的距离为![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=![]() 的定义域为(-1,1),满足f(-x)=-f(x),且
的定义域为(-1,1),满足f(-x)=-f(x),且![]() .
.
(1)求函数f(x)的解析式;
(2)证明f(x)在(-1,1)上是增函数;
(3)解不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是实数,
是实数,![]() ,
,
(1)若函数![]() 为奇函数,求
为奇函数,求![]() 的值;
的值;
(2)试用定义证明:对于任意![]() ,
,![]() 在
在![]() 上为单调递增函数;
上为单调递增函数;
(3)若函数![]() 为奇函数,且不等式
为奇函数,且不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修![]() :不等式选讲
:不等式选讲
已知函数f(x)=|2x+3|+|2x﹣1|.
(Ⅰ)求不等式f(x)<8的解集;
(Ⅱ)若关于x的不等式f(x)≤|3m+1|有解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产A,B两种产品,根据市场调查与市场预测,知A产品的利润与投资成正比,其关系如图1,B产品的利润与投资的算术平方根成正比,其关系如图2.(注:所示图中的横坐标表示投资金额,单位:万元)

图1 图2
(1)分别将A,B两种产品的利润表示为投资的函数关系式;
(2)该企业已筹集10万元资金,并全部投入A,B两种产品的生产,问:怎样分配这10万元资金,才能使企业获得最大利润,最大利润为多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com