
【题目】如图,在三棱锥![]() 中,
中,![]() ,点
,点![]() 分别是棱
分别是棱![]() 上的点满足
上的点满足![]() .
.
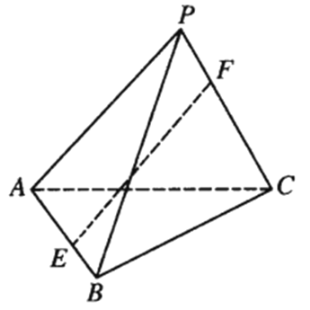
(Ⅰ)证明:![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(Ⅰ)见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,由平面几何的知识可得
,由平面几何的知识可得![]() 、
、![]() ,再由线面垂直的判定与性质即可得证;
,再由线面垂直的判定与性质即可得证;
(Ⅱ)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,由面面垂直的判定与性质可得
,由面面垂直的判定与性质可得![]() 平面
平面![]() ,即可得
,即可得![]() 是所求线面角,由平面几何的知识结合余弦定理可得线段
是所求线面角,由平面几何的知识结合余弦定理可得线段![]() 、
、![]() 的长度,即可得解.
的长度,即可得解.
(Ⅰ)证明:取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,因为
,因为![]() ,
,
故![]() ,
,![]() 且
且![]() ,所以
,所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,故
,故![]() ;
;
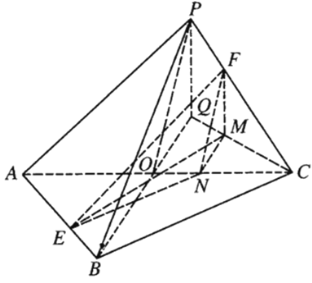
(Ⅱ)由(Ⅰ)知![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,
,
故平面![]() 平面
平面![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,
,
由平面![]() 平面
平面![]() 可得
可得![]() 平面
平面![]() ,
,
过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,
,
所以![]() 平面
平面![]() ,即
,即![]() 是
是![]() 与平面
与平面![]() 所成的角.
所成的角.
过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 、
、![]() ,
,
因为![]() ,
,![]() ,
,
所以![]() 即
即![]() ,
,
所以![]() ,所以
,所以![]() ,
,![]()
因为![]() ,所以
,所以![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
由![]() ,
,![]() 得
得![]() ,
,![]() ,
,
又由![]() 得
得![]() ,
,
所以由余弦定理得![]() ,
,
故![]() ,
,
所以有![]() ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数,且
为参数,且![]() ,在以
,在以![]() 为极点、
为极点、![]() 轴的非负半轴为极轴的极坐标系(两种坐标系取相同的单位长度)中,曲线
轴的非负半轴为极轴的极坐标系(两种坐标系取相同的单位长度)中,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,设直线
,设直线![]() 经过定点
经过定点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 、
、![]() 两点.
两点.
(Ⅰ)求点![]() 的直角坐标及曲线
的直角坐标及曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)求证:不论![]() 为何值时,
为何值时,![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】武汉出现的新型冠状病毒是一种可以通过飞沫传播的变异病毒,某药物研究所为筛查该新型冠状病毒,需要检验血液是否为阳性,现有![]() 份血液样本,每份样本取到的可能性均等,有以下两种检验方式:①逐份检验,则需要检验n次;②混合检验,将其中
份血液样本,每份样本取到的可能性均等,有以下两种检验方式:①逐份检验,则需要检验n次;②混合检验,将其中![]() 份血液样本分别取样混合在一起检验.若检验结果为阴性,这k份血液全为阴性,因此这k份血液样本检验一次就够了,如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份血液再逐份检验,此时这k份血液的检验次数总共为
份血液样本分别取样混合在一起检验.若检验结果为阴性,这k份血液全为阴性,因此这k份血液样本检验一次就够了,如果检验结果为阳性,为了明确这k份血液究竟哪几份为阳性,就要对这k份血液再逐份检验,此时这k份血液的检验次数总共为![]() 次.假设在接受检验的血液样本中,每份样本的检验结果是阴性还是阳性都是独立的,且每份样本是阳性结果的概率为
次.假设在接受检验的血液样本中,每份样本的检验结果是阴性还是阳性都是独立的,且每份样本是阳性结果的概率为![]() .
.
(1)假设有5份血液样本,其中只有2份为阳性,若采取逐份检验方式,求恰好经过2次检验就能把阳性样本全部检验出来的概率;
(2)现取其中![]() 份血液样本,记采用逐份检验方式,样本需要检验的次数为
份血液样本,记采用逐份检验方式,样本需要检验的次数为![]() ,采用混合检验方式,样本需要检验的总次数为
,采用混合检验方式,样本需要检验的总次数为![]() .
.
(i)试运用概率统计知识,若![]() ,试求P关于k的函数关系式
,试求P关于k的函数关系式![]() ;
;
(ii)若![]() ,采用混合检验方式可以使得这k份血液样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求k的最大值.
,采用混合检验方式可以使得这k份血液样本需要检验的总次数的期望值比逐份检验的总次数期望值更少,求k的最大值.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年4月,河北、辽宁、江苏、福建、湖北、湖南、广东、重庆等8省市发布高考综合改革实施方案,决定从2018年秋季入学的高中一年级学生开始实施“![]() ”高考模式.所谓“
”高考模式.所谓“![]() ”,即“3”是指考生必选语文、数学、外语这三科;“1”是指考生在物理、历史两科中任选一科;“2”是指考生在生物、化学、思想政治、地理四科中任选两科.
”,即“3”是指考生必选语文、数学、外语这三科;“1”是指考生在物理、历史两科中任选一科;“2”是指考生在生物、化学、思想政治、地理四科中任选两科.
(1)若某考生按照“![]() ”模式随机选科,求选出的六科中含有“语文,数学,外语,物理,化学”的概率.
”模式随机选科,求选出的六科中含有“语文,数学,外语,物理,化学”的概率.
(2)新冠疫情期间,为积极应对“![]() ”新高考改革,某地高一年级积极开展线上教学活动.教育部门为了解线上教学效果,从当地不同层次的学校中抽取高一学生2500名参加语数外的网络测试,并给前400名颁发荣誉证书,假设该次网络测试成绩服从正态分布,且满分为450分.
”新高考改革,某地高一年级积极开展线上教学活动.教育部门为了解线上教学效果,从当地不同层次的学校中抽取高一学生2500名参加语数外的网络测试,并给前400名颁发荣誉证书,假设该次网络测试成绩服从正态分布,且满分为450分.
①考生甲得知他的成绩为270分,考试后不久了解到如下情况:“此次测试平均成绩为171分,351分以上共有57人”,请用你所学的统计知识估计甲能否获得荣誉证书,并说明理由;
②考生丙得知他的实际成绩为430分,而考生乙告诉考生丙:“这次测试平均成绩为201分,351分以上共有57人”,请结合统计学知识帮助丙同学辨别乙同学信息的真伪,并说明理由.
附:![]() ;
;
![]() ;
;
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
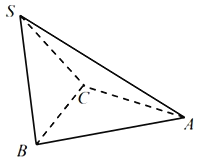
【题目】如图所示,三棱锥S一ABC中,△ABC与△SBC都是边长为1的正三角形,二面角A﹣BC﹣S的大小为![]() ,若S,A,B,C四点都在球O的表面上,则球O的表面积为( )
,若S,A,B,C四点都在球O的表面上,则球O的表面积为( )
A.![]() πB.
πB.![]() πC.
πC.![]() πD.3π
πD.3π
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)的图象的一个最高点为(![]() ),与之相邻的一个对称中心为
),与之相邻的一个对称中心为![]() ,将f(x)的图象向右平移
,将f(x)的图象向右平移![]() 个单位长度得到函数g(x)的图象,则( )
个单位长度得到函数g(x)的图象,则( )
A.g(x)为偶函数
B.g(x)的一个单调递增区间为![]()
C.g(x)为奇函数
D.函数g(x)在![]() 上有两个零点
上有两个零点
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地出现了虫害,农业科学家引入了“虫害指数”数列![]() ,
,![]() 表示第
表示第![]() 周的虫害的严重程度,虫害指数越大,严重程度越高,为了治理虫害,需要环境整治、杀灭害虫,然而由于人力资源有限,每周只能采取以下两个策略之一:
周的虫害的严重程度,虫害指数越大,严重程度越高,为了治理虫害,需要环境整治、杀灭害虫,然而由于人力资源有限,每周只能采取以下两个策略之一:
策略![]() :环境整治,“虫害指数”数列满足
:环境整治,“虫害指数”数列满足![]() ;
;
策略![]() :杀灭害虫,“虫害指数”数列满足
:杀灭害虫,“虫害指数”数列满足![]() ;
;
当某周“虫害指数”小于1时,危机就在这周解除.
(1)设第一周的虫害指数![]() ,用哪一个策略将使第二周的虫害严重程度更小?
,用哪一个策略将使第二周的虫害严重程度更小?
(2)设第一周的虫害指数![]() ,如果每周都采用最优的策略,虫害的危机最快在第几周解除?
,如果每周都采用最优的策略,虫害的危机最快在第几周解除?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com