
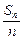 )|n∈N*},B={(x,y)|
)|n∈N*},B={(x,y)|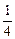 x2-y2=1,x,y∈R}.
x2-y2=1,x,y∈R}.

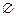 .
.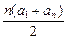 ,则
,则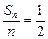 (a1+an),这表明点(an,
(a1+an),这表明点(an,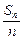 )的
)的 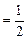 (x+a1),于是点(an,
(x+a1),于是点(an, 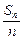 )均在直线y=
)均在直线y=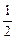 x+
x+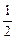 a1上
a1上
 设(x,y)∈A∩B,则(x,y)中的坐标x,y应是方程组
设(x,y)∈A∩B,则(x,y)中的坐标x,y应是方程组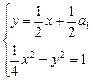 的解,由方程组消去y得:2a1x+a12=-4(*),当a1=0时,方程(*)无解,此时A∩B=
的解,由方程组消去y得:2a1x+a12=-4(*),当a1=0时,方程(*)无解,此时A∩B=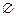 ;当a1≠0时,方程(*)只有一个解x=
;当a1≠0时,方程(*)只有一个解x=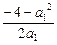 ,此时,方程组也只有一解
,此时,方程组也只有一解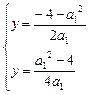 ,故上述方程组至多有一解
,故上述方程组至多有一解

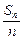 >0,这时集合A中的元素作为点的坐标,其横、纵坐标均为正,另外,由于a1=1≠0
>0,这时集合A中的元素作为点的坐标,其横、纵坐标均为正,另外,由于a1=1≠0 如果A∩B≠
如果A∩B≠ ,那么据(2)的结论,A∩B中至多有一个元素(x0,y0),而x0=
,那么据(2)的结论,A∩B中至多有一个元素(x0,y0),而x0=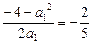 <0,y0=
<0,y0=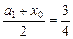 <0,这样的(x0,y0)
<0,这样的(x0,y0)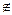 A,产生矛盾,故a1=1,d=1时A∩B=
A,产生矛盾,故a1=1,d=1时A∩B=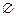 ,所以a1≠0时,一定有A∩B≠
,所以a1≠0时,一定有A∩B≠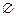 是不正确的.
是不正确的.

科目:高中数学 来源:不详 题型:解答题
| 2 |
| 1 | ||
3-4
|
9-4
|
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com