，2），则
。
口算能手系列答案科目：高中数学 来源：福建省福州八中2007－2008高三毕业班第三次质量检查数学试题(理科) 题型：044
设函数f(x)＝3x2＋1，g(x)＝2x，现有数列{an}满足条件：对于n∈N*，an＞0且f(an＋1)－f(an)＝g(an+1＋
)，又设数列{bn}满足条件：bn＝
(a＞0且a≠1，n∈N*)．
(1)求证：数列{an}为等比数列；
(2)求证：数列
是等差数列；
(3)设k，L∈N**，且k＋L＝5，bk＝
，bL＝
，求数列{bn}的通项公式；
(4)如果k＋L＝M0(k，L∈N＋，M0＞3且M0是奇数)，且bk＝
，bL＝
，求从第几项开始an＞1恒成立．
查看答案和解析>>
科目：高中数学 来源：湖南省长沙市第一中学2011届高三第三次月考理科数学试题 题型：013
函数y＝
(x)是函数y＝f(x)的导函数，且函数y＝f(x)在点p(x0，f(x0))处的切线为l：y＝g(x)＝
(x0)(x－x0)＋f(x0)，F(x)＝f(x)－g(x)，如果函数y＝f(x)在区间[a，b]上的图像如图所示，且a＜x0＜b，那么
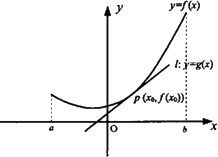
(x0)＝0，x＝x0是F(x)的极大值点
(x0)＝0，x＝x0是F(x)的极小值点
(x0)≠0，x＝x0不是F(x)极值点
(x0)≠0，x＝x0是F(x)极值点
查看答案和解析>>
科目：高中数学 来源：山西省山大附中2012届高三4月月考数学理科试题 题型：013
函数f(x)的定义域为D，若存在非零实数l使得对于任意x∈M(M
D)，有x＋l∈D，且f(x＋l)≥f(x)，则称f(x)为M上的l高调函数．如果定义域为R的函数f(x)是奇函数，当x≥0时，f(x)＝|x－a2|－a2，且f(x)为R上的4高调函数，那么实数a的取值范围是
A．0＜a＜1．
B．－2＜a＜2
C．－1≤a≤1
D．－2≤a≤2
查看答案和解析>>
科目：高中数学 来源： 题型：
设函数f(x)的定义域为D，若存在非零实数l使得对于任意x∈M(M⊆D)，有x＋l∈D，且f(x＋l)≥f(x)，则称f(x)为M上的l高调函数.
(1)如果定义域为[－1，＋∞)的函数f(x)＝x2为[－1，＋∞)上的m高调函数，求实数m的取值范围.
(2)如果定义域为R的函数f(x)是奇函数，当x≥0时，f(x)＝|x－a2|－a2，且f(x)为R上的4高调函数，求实数a的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
已知函数f(x)＝x3＋x－16.
(1)求曲线y＝f(x)在点(2，－6)处的切线的方程；
(2)直线l为曲线y＝f(x)的切线，且经过原点，求直线l的方程及切点坐标；
(3)如果曲线y＝f(x)的某一切线与直线y＝－
x＋3垂直，求切点坐标与切线的方程．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
根据等比数列的求和公式即可求的
