[题目]已知曲线在点处的切线斜率为0.(1)讨论函数的单调性,(2)在区间上没有零点.求实数的取值范围．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知曲线在点处的切线斜率为0.

（1）讨论函数的单调性；

（2）在区间上没有零点，求实数的取值范围．

【答案】（Ⅰ）单调递增区间是，单调递减区间是．（Ⅱ）．

【解析】试题分析：（1）由的定义域为，得，因为，所以，代入，令，，即可求解函数的单调区间；

（2）由函数得可得在上是减函数，在上为增函数，由在区间上没有零点，得在上恒成立，根据，得，设，求解函数的最值，即可得到结论。

试题解析：

解：（Ⅰ）的定义域为，．

因为，所以，，．

令，得，令，得，

故函数的单调递增区间是，单调递减区间是．

（Ⅱ），由，得，

设，所以在上是减函数，在上为增函数．

因为在区间上没有零点，所以在上恒成立，

由，得，令，则．

当时，，所以在上单调递减；

所以当时，，故，即．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

【题目】已知函数f(x)＝ax3－bx2＋(2－b)x＋1在x＝x1处取得极大值，在x＝x2处取得极小值，且0＜x1＜1＜x2＜2.

(1)证明：a＞0；

(2)若z＝a＋2b，求z的取值范围.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】网络购物已经成为一种时尚，电商们为了提升知名度，加大了在媒体上的广告投入．经统计，近五年某电商在媒体上的广告投入费用x（亿元）与当年度该电商的销售收入y（亿元）的数据如下表：）：

年份	2012年	2013年	2014	2015	2016
广告投入x	0.8	0.9	1	1.1	1.2
销售收入y	16	23	25	26	30

（1）求y关于x的回归方程；（2）2017年度该电商准备投入广告费1.5亿元，

利用（1）中的回归方程，预测该电商2017年的销售收入．

附：回归直线的斜率和截距的最小二乘估计公式分别为：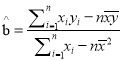

，选用数据：，

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】过点作抛物线的两条切线, 切点分别为, .

（1）证明: 为定值;

（2）记△的外接圆的圆心为点, 点是抛物线的焦点, 对任意实数, 试判断以为直径的圆是否恒过点? 并说明理由.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】选修4-4；坐标系与参数方程

在直角坐标系中，直线的参数方程为（为参数）．在以坐标原点为极点，轴正半轴为极轴的极坐标中，曲线．

（Ⅰ）求直线的普通方程和曲线的直角坐标方程．

（Ⅱ）求曲线上的点到直线的距离的最大值．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】有一种新型的洗衣液，去污速度特别快．已知每投放k(1≤k≤4，且k∈R)个单位的洗衣液在一定量水的洗衣机中，它在水中释放的浓度y(克/升)随着时间x(分钟)变化的函数关系式近似为y＝k·f(x)，其中f(x)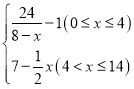＝若多次投放，则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和．根据经验，当水中洗衣液的浓度不低于4(克/升)时，它才能起到有效去污的作用．