已知向量
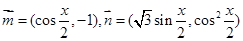
,设函数
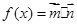
(1)求
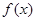
在区间
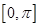
上的零点;
(2)在
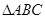
中,角
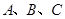
的对边分别是
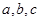
,且满足
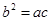
,求
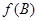
的取值范围.
试题分析:(1)先由平面向量数量积的坐标表示得到
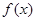
,然后由三角函数的倍角公式进行降次,再将函数
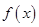
的解析式化为
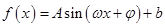
的形式.令
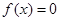
,在区间
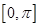
解得
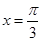
或
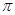
,即得到零点
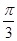
、
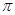
;(2)由条件及余弦定理,通过基本不等式可得
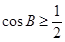
,又根据角
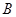
是三角形内角,从而得到其范围,再代入即可得
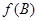
的取值范围.
试题解析:因为向量
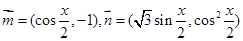
,函数
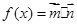
.
所以
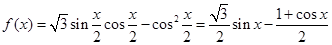
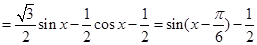
3分
(1)由
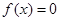
,得
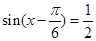
.
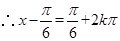
,
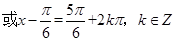
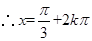
,
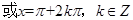
又
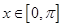
,
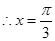
或
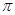
.
所以
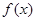
在区间
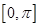
上的零点是
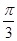
、
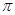
. 6分
(2)在
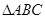
中,
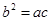
,所以
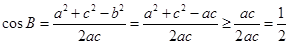
.
由
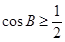
且
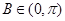
,得

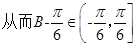
10分
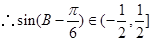
,
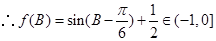
12分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
在
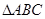
中,角
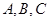
的对边分别为
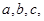
向量
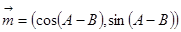
,
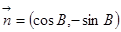
,且
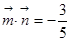
.
(1)求
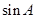
的值;
(2)若
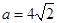
,
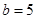
,求角
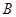
的大小及向量
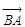
在
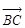
方向上的投影.
查看答案和解析>>
科目:高中数学
来源:不详
题型:解答题
已知
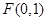
是中心在坐标原点
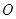
的椭圆

的一个焦点,且椭圆

的离心率
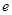
为
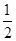
.
(Ⅰ)求椭圆

的方程;
(Ⅱ)设:
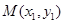
、
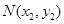
为椭圆

上不同的点,直线
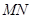
的斜率为
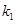
;
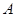
是满足
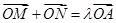
(
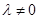
)的点,且直线
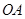
的斜率为
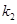
.
①求
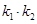
的值;
②若
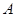
的坐标为
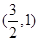
,求实数
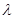
的取值范围.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
在
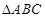
中,
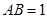
,
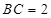
,
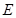
为
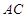
的中点 ,则
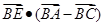
=( )
| A.3 | B.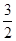 | C.-3 | D.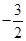 |
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
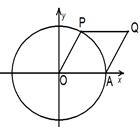
如图A是单位圆与

轴的交点,点

在单位圆上,

,

,四边形
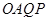
的面积为

,当
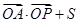
取得最大值时

的值和最大值分别为( )
查看答案和解析>>
科目:高中数学
来源:不详
题型:填空题
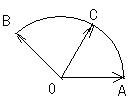
给定两个长度为1的平面向量
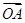
和
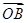
,它们的夹角为
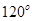
.如图所示,点C在以O为圆心的圆弧
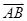
上变动.若
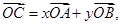
其中
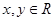
,则
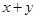
的最大值是________.
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
设点

、

、

且

满足

,则

取得最小值时,点B的个数是( )
查看答案和解析>>

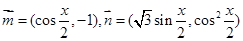 ,设函数
,设函数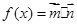
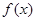 在区间
在区间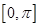 上的零点;
上的零点;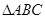 中,角
中,角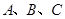 的对边分别是
的对边分别是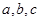 ,且满足
,且满足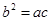 ,求
,求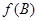 的取值范围.
的取值范围. 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案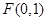 是中心在坐标原点
是中心在坐标原点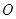 的椭圆
的椭圆 的一个焦点,且椭圆
的一个焦点,且椭圆 的离心率
的离心率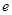 为
为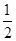 .
. 的方程;
的方程;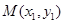 、
、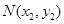 为椭圆
为椭圆 上不同的点,直线
上不同的点,直线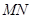 的斜率为
的斜率为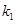 ;
;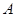 是满足
是满足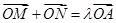 (
(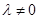 )的点,且直线
)的点,且直线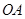 的斜率为
的斜率为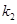 .
.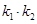 的值;
的值;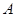 的坐标为
的坐标为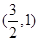 ,求实数
,求实数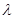 的取值范围.
的取值范围.