练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    一名小学生的年龄和身高（单位：cm）的数据如下表：
    年龄 6789
    身高 118126136144
    由散点图可知，身高y与年龄x之间的线性回归方程为
    ?
    y
    =8.8x+
    ?
    a
    ，预测该学生10岁时的身高为（　　）
    A．154B．153C．152D．151
    由题意，
    .
    x
    =7.5，
    .
    y
    =131
    代入线性回归直线方程为
    ?
    y
    =8.8x+
    ?
    a
    ，131=8.8×7.5+
    ?
    a
    ，可得
    ?
    a
    =65，
    ∴
    ?
    y
    =8.8x+65
    ∴x=10时，
    ?
    y
    =8.8×10+65    =153
    故选B．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：单选题

    已知的取值如下表所示：

    		2
    		3
    		4

    		6
    		4
    		5
            如果与呈线性相关，且线性回归方程为，则
    (A)              (B)                 (C)            (D)

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

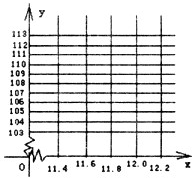
    某超市在一段时间内的某种商品的价格x（元）与销售量y（kg）之间的一组数据如下表所示：
    价格x（元）11.411.611.812.012.2
    销售量y（kg）112110107105103
    （Ⅰ）画出散点图；
    （Ⅱ）求出y对x的回归的直线方程；
    （Ⅲ）当价格定为11.9元时，预测销售量大约是多少？
    b
    =
    n
    i=1
    (x1-
    .
    x
    )(y1-
    .
    y
    )
    n
    i=1
    (x1-
    .
    x
    )    2
    =
    n
    i=1
    x1y1-n
    .
    x
    .
    y
    n
    i=1
    x    		21
    -n
    .
    x
    2
    ．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某连锁经营公司所属5个零售店某月的销售额和利润额如下表：
    商店名称ABCDE
    销售额x/万元35679
    利润额y/万元23345
    （1）画出销售额和利润额的散点图．
    （2）若销售额和利润额具有相关关系，试计算利润额y对销售额x的回归直线方程．
    （3）估计要达到1万元的利润额，销售额大约为多少万元？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知两个变量x与y之间具有线性相关关系，5次试验的观测数据如下：
    x100120140160180
    y4554627592
    那么变量y关于x的回归直线方程只可能是（　　）
    A．
    y
    =0.575x-14.9    		B．
    y
    =0.572x-13.9
    C．
    y
    =0.575x-12.9    		D．
    y
    =0.572x-14.9

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    两变量x和y成线性相关关系，对应数据如表，若线性回归方程为：
    y
    =1.9x+
    a
    ．则
    a
    =______．
    x22.533.54
    y44.86.26.98.1

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某种产品的广告费用支出X与销售额之间有如下的对应数据：
    x24568
    y3040605070
    （1）画出散点图；
    （2）求回归直线方程；
    （3）据此估计广告费用为10销售收入y的值．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    废品率x%与每吨生铁成本y（元）之间的回归直线方程为
    ?
    y
    =234+3x，表明（　　）
    A．废品率每增加1%，生铁成本增加3x元
    B．废品率每增加1%，生铁成本每吨增加3元
    C．废品率每增加1%，生铁成本增加234元
    D．废品率不变，生铁成本为234元

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    改革开放以来，我国高等教育事业有了突飞猛进的发展，有人记录了某村2001到2005年五年间每年考入大学的人数，为了方便计算，2001年编号为1，2002年编号为2，…，2005年编号为5，数据如下：
    年份（x）12345
    人数（y）3581113
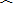    （1）从这5年中随机抽取两年，求考入大学的人数至少有1年多于10人的概率．
    （2）根据这5年的数据，利用最小二乘法求出y关于x的回归方程
    y
    =
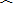    b
    x+
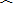    a
    ，并计算第8年的估计值．
    参考：用最小二乘法求线性回归方程系数公式
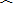    b
    =
    n
    i=1
    xiyi-n
    .
    x
    •
    .
    y
    n
    i=1
    xi2-n
    .
    x
    2
    ，
    a
    =
    .
    y
    -b
    .
    x
    ．

    查看答案和解析>>

    同步练习册答案