
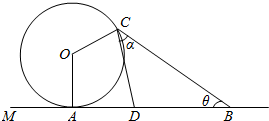
 如图,在一条景观道的一端有一个半径为50米的圆形摩天轮O,逆时针15分钟转一圈,从A处进入摩天轮的座舱,OA垂直于地面AM,在距离A处150米处设置了一个望远镜B.
如图,在一条景观道的一端有一个半径为50米的圆形摩天轮O,逆时针15分钟转一圈,从A处进入摩天轮的座舱,OA垂直于地面AM,在距离A处150米处设置了一个望远镜B.分析 (1)因为摩天轮做匀速转动,逆时针15分钟转一圈,可得5分钟转过120°,过点C作CH⊥AB于点H,利用解三角形可得望远镜B的仰角θ;
(2)由题意可求CD,利用正弦定理即可解得BD的长度.
解答 (本题(14分),第1小题(8分),第2小题6分)
解:(1)∵逆时针15分钟转一圈,
∴5分钟转过120°(2分)
过点C作CH⊥AB于点H,
则CH=50+50•sin(120°-90°)=75(2分)
$BH=150-50•cos({120°-90°})=150-25\sqrt{3}$(2分)
∴$tanθ=\frac{CH}{BH}=\frac{75}{{150-25\sqrt{3}}}=\frac{{\sqrt{3}}}{{2\sqrt{3}-1}}=\frac{{6+\sqrt{3}}}{11}$,
∴$θ=arctan\frac{{6+\sqrt{3}}}{11}≈35°$(2分)
答:望远镜的仰角θ设置为35°
(2)在△BCD中,θ=35°,α=45°,
∴∠CDH=80°(2分)
∴$CD=\frac{CH}{sin80°}=\frac{75}{sin80°}$
由正弦定理得:$\frac{BD}{sinα}=\frac{CD}{sinθ}$(2分)
∴$BD=\frac{CD•sinα}{sinθ}=\frac{75•sin45°}{sin80°•sin35°}≈94$(2分)
答:绿化带的长度为94米.
点评 本题考查了已知三角函数模型的应用问题,解答本题的关键是作出正确的示意图,然后再由三角形中的相关知识进行求解,解题时要注意综合利用所学知识与题中的条件,求解三角形的边与角,是中档题.


科目:高中数学 来源: 题型:选择题
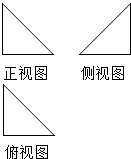 一个空间几何体的三视图如图所示,其正视图、侧视 图、俯视图均为等腰直角三角形,且直角边长都为1,则它的外接球的表面积是( )
一个空间几何体的三视图如图所示,其正视图、侧视 图、俯视图均为等腰直角三角形,且直角边长都为1,则它的外接球的表面积是( )| A. | 3π | B. | π | C. | 2π | D. | 4π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 金红石(TiO2)的晶胞如图所示,图中色点代表钛原子,黑点代表氧原子.长方体的8个顶点和中心是钛原子,4个氧原子的位置是A(0.31a,0.31b,0),B(0.69a,0.69b,0),C(0.81a,0,0.5c)和D(0.19a,0.81b,0.5c).中心处钛原子与A处氧原子间的距离叫做键长.当a=b时,试求键长.
金红石(TiO2)的晶胞如图所示,图中色点代表钛原子,黑点代表氧原子.长方体的8个顶点和中心是钛原子,4个氧原子的位置是A(0.31a,0.31b,0),B(0.69a,0.69b,0),C(0.81a,0,0.5c)和D(0.19a,0.81b,0.5c).中心处钛原子与A处氧原子间的距离叫做键长.当a=b时,试求键长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com