
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,点
,点![]() 为椭圆上一点.
为椭圆上一点.
(1)求椭圆C的方程;
(2)已知两条互相垂直的直线![]() ,
,![]() 经过椭圆
经过椭圆![]() 的右焦点
的右焦点![]() ,与椭圆
,与椭圆![]() 交于
交于![]() 四点,求四边形
四点,求四边形![]() 面积的的取值范围.
面积的的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)由题意可得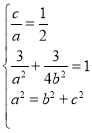 ,解得进而得到椭圆的方程;(2)设出直线l1,l2的方程,直线和椭圆方程联立,运用韦达定理和弦长公式,分别求得|AB|,|MN|,再由四边形的面积公式,化简整理计算即可得到取值范围.
,解得进而得到椭圆的方程;(2)设出直线l1,l2的方程,直线和椭圆方程联立,运用韦达定理和弦长公式,分别求得|AB|,|MN|,再由四边形的面积公式,化简整理计算即可得到取值范围.
(1)由题意可得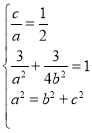 ,解得a2=4,b2=3,c2=1
,解得a2=4,b2=3,c2=1
故椭圆C的方程为![]() ;
;
(2)当直线l1的方程为x=1时,此时直线l2与x轴重合,
此时|AB|=3,|MN|=4,
∴四边形AMBN面积为S![]() |AB||MN|=6.
|AB||MN|=6.
设过点F(1,0)作两条互相垂直的直线l1:x=ky+1,直线l2:x![]() y+1,
y+1,
由x=ky+1和椭圆![]() 1,可得(3k2+4)y2+6ky﹣9=0,
1,可得(3k2+4)y2+6ky﹣9=0,
判别式显然大于0,y1+y2![]() ,y1y2
,y1y2![]() ,
,
则|AB|![]()
![]()
![]() ,
,
把上式中的k换为![]() ,可得|MN|
,可得|MN|![]()
则有四边形AMBN面积为S![]() |AB||MN|
|AB||MN|![]()
![]()
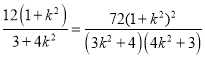 ,
,
令1+k2=t,则3+4k2=4t﹣1,3k2+4=3t+1,
则S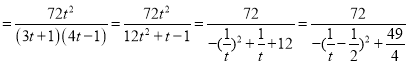 ,
,
∴t>1,
∴0![]() 1,
1,
∴y=﹣(![]() )2
)2![]() ,在(0,
,在(0,![]() )上单调递增,在(
)上单调递增,在(![]() ,1)上单调递减,
,1)上单调递减,
∴y∈(12,![]() ],
],
∴S∈[![]() ,6)
,6)
故四边形PMQN面积的取值范围是![]()


科目:高中数学 来源: 题型:
【题目】已知函数![]() 的相邻两对称轴间的距离为
的相邻两对称轴间的距离为![]() ,若将
,若将![]() 的图像先向左平移
的图像先向左平移![]() 个单位,再向下平移
个单位,再向下平移![]() 个单位,所得的函数
个单位,所得的函数![]() 为奇函数.
为奇函数.
(1)求![]() 的解析式;
的解析式;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不等实根,求实数
上有两个不等实根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】这是今年双十一的两道题目,第一题是双十一之前网上流传甚广的小明买卫衣问题,第二题是有关某老师的双十一战果.
(1)小明想在双十一买价值399的卫衣,已知付定金20元有订金三倍膨胀活动,但仅限当天0到2点,2点以后订金可抵用50元,但有付尾款前500名免定金活动,同时该店铺有399减20和299减10的优惠券(其使用门槛是订金![]() 尾款
尾款![]() 订金膨胀优惠金额大于等于优惠券),还有一种379减20和279减10的折扣券(其使用门槛是尾款
订金膨胀优惠金额大于等于优惠券),还有一种379减20和279减10的折扣券(其使用门槛是尾款![]() 膨胀优惠金额大于等于折扣券面额),优惠和折扣只能选一种,求小明最低多少钱能买到这件卫衣?如果你是小明,你会选择怎样购买?
膨胀优惠金额大于等于折扣券面额),优惠和折扣只能选一种,求小明最低多少钱能买到这件卫衣?如果你是小明,你会选择怎样购买?
(2)某老师在双十一前花1元,抢到了某商家满![]() 的一张优惠券,该商家没有订金膨胀活动,但该商家有多买多优惠活动:满3件9折,5件8折,10件及以上7折,同时可用淘宝
的一张优惠券,该商家没有订金膨胀活动,但该商家有多买多优惠活动:满3件9折,5件8折,10件及以上7折,同时可用淘宝![]() 的购物津贴(可跨店满减,店铺优惠后参加该活动,但运费不在其中),现已知该老师本单共花了
的购物津贴(可跨店满减,店铺优惠后参加该活动,但运费不在其中),现已知该老师本单共花了![]() 元(1是买券钱,119.78是双十一付款,其中含运费6元).
元(1是买券钱,119.78是双十一付款,其中含运费6元).
请问:该老师本次购买的商品价值最低多少?最高多少?(按商家标示的淘宝价格计算,精确到元即可,已知该老师用了![]() 券)
券)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() 为等边三角形,
为等边三角形,![]() 是线段
是线段![]() 上的一点,且
上的一点,且![]() 平面
平面![]() .
.

(1)求证:![]() 为
为![]() 的中点;
的中点;
(2)若![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
,![]() ,
,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,
,![]() ,求三棱锥
,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为庆祝党的98岁生日,某高校组织了“歌颂祖国,紧跟党走”为主题的党史知识竞赛。从参加竞赛的学生中,随机抽取40名学生,将其成绩分为六段![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,到如图所示的频率分布直方图.
,到如图所示的频率分布直方图.

(1)求图中![]() 的值及样本的中位数与众数;
的值及样本的中位数与众数;
(2)若从竞赛成绩在![]() 与
与![]() 两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于
两个分数段的学生中随机选取两名学生,设这两名学生的竞赛成绩之差的绝对值不大于![]() 分为事件
分为事件![]() ,求事件
,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点也是椭圆
的焦点也是椭圆![]() 的一个焦点,点
的一个焦点,点![]() 在椭圆短轴
在椭圆短轴![]() 上,且
上,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 为椭圆
为椭圆![]() 上的一个不在
上的一个不在![]() 轴上的动点,
轴上的动点,![]() 为坐标原点,过椭圆的右焦点
为坐标原点,过椭圆的右焦点![]() 作
作![]() 的平行线,交曲线
的平行线,交曲线![]() 于
于![]() 两点,求
两点,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右顶点为
的右顶点为![]() ,上顶点为
,上顶点为![]() ,右焦点为
,右焦点为![]() .连接
.连接![]() 并延长与椭圆
并延长与椭圆![]() 相交于点
相交于点![]() ,且
,且![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,直线
,直线![]() 分别与直线
分别与直线![]() 相交于点
相交于点![]() ,点
,点![]() .若
.若![]() 的面积是
的面积是![]() 的面积的2倍,求直线
的面积的2倍,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com