
【题目】某校要在一条水泥路边安装路灯,其中灯杆的设计如图所示,AB为地面,CD,CE为路灯灯杆,CD⊥AB,∠DCE=![]() ,在E处安装路灯,且路灯的照明张角∠MEN=
,在E处安装路灯,且路灯的照明张角∠MEN=![]() .已知CD=4m,CE=2m.
.已知CD=4m,CE=2m.
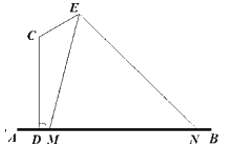
(1)当M,D重合时,求路灯在路面的照明宽度MN;
(2)求此路灯在路面上的照明宽度MN的最小值.
 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=3上的一动点M在x轴上的投影为N,点P满足![]() .
.
(1)求动点P的轨迹C的方程;
(2)若直线l与圆O相切,且交曲线C于点A,B,试求|AB|的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某景区内有一半圆形花圃,其直径AB为6,O是圆心,且OC⊥AB.在OC上有一座观赏亭Q,其中∠AQC=![]() ,.计划在
,.计划在![]() 上再建一座观赏亭P,记∠POB=θ
上再建一座观赏亭P,记∠POB=θ![]() .
.
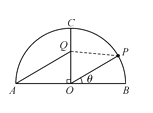
(1)当θ=![]() 时,求∠OPQ的大小;
时,求∠OPQ的大小;
(2)当∠OPQ越大时,游客在观赏亭P处的观赏效果越佳,求游客在观赏亭P处的观赏效果最佳时,角θ的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公园内有一块以![]() 为圆心半径为
为圆心半径为![]() 米的圆形区域.为丰富市民的业余文化生活,现提出如下设计方案:如图,在圆形区域内搭建露天舞台,舞台为扇形
米的圆形区域.为丰富市民的业余文化生活,现提出如下设计方案:如图,在圆形区域内搭建露天舞台,舞台为扇形![]() 区域,其中两个端点
区域,其中两个端点![]() ,
,![]() 分别在圆周上;观众席为梯形
分别在圆周上;观众席为梯形![]() 内切在圆
内切在圆![]() 外的区域,其中
外的区域,其中![]() ,
,![]() ,且
,且![]() ,
,![]() 在点
在点![]() 的同侧.为保证视听效果,要求观众席内每一个观众到舞台
的同侧.为保证视听效果,要求观众席内每一个观众到舞台![]() 处的距离都不超过
处的距离都不超过![]() 米.设
米.设![]() ,
,![]() .问:对于任意
.问:对于任意![]() ,上述设计方案是否均能符合要求?
,上述设计方案是否均能符合要求?

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市2010年4月1日—4月30日对空气污染指数的监测数据如(主要污染物为可吸入颗粒物):61,76,70,56,81,91,92,91,75,81,88,67,101,103,95,91,77,86,83,82,82,64,79,86,85,75,71,49,45.
样本频率分布表:
分组 | 频数 | 频率 |
[41,51) | 2 | |
[51,61) | 1 | |
[61,71) | 4 | |
[71,81) | 6 | |
[81,91) | 10 | |
[91,101) | ||
[101,111) | 2 |
(1) 完成频率分布表;
(2)作出频率分布直方图;
(3)根据国家标准,污染指数在0~50之间时,空气质量为优:在51~100之间时,为良;在101~150之间时,为轻微污染;在151~200之间时,为轻度污染.请你依据所给数据和上述标准,对该市的空气质量给出一个简短评价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,a,b,c分别是角A,B,C的对边,且acosC=(2b﹣c)cosA.
(1)若![]() 3,求△ABC的面积;
3,求△ABC的面积;
(2)若∠B<∠C,求2cos2B+cos2C的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,且acos C+![]() asin C-b-c=0.
asin C-b-c=0.
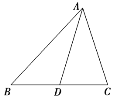
(1)求A;
(2)若AD为BC边上的中线,cos B=![]() ,AD=
,AD=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的离心率为
的离心率为![]() ,右准线方程为
,右准线方程为![]() ,
,![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右顶点,过右焦点
的左、右顶点,过右焦点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点.
两点.
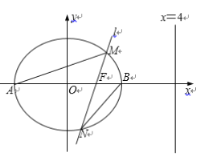
(1)求椭圆![]() 的标准方程.
的标准方程.
(2)记![]() 、
、![]() 的面积分别为
的面积分别为![]() 、
、![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
(3)设线段![]() 的中点为
的中点为![]() ,直线
,直线![]() 与右准线相交于点
与右准线相交于点![]() ,记直线
,记直线![]() 、
、![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com