
【题目】已知椭圆![]() 的中心在原点,对称轴为坐标轴,椭圆
的中心在原点,对称轴为坐标轴,椭圆![]() 与直线
与直线![]() 相切于点
相切于点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() :
: ![]() 与椭圆相交于
与椭圆相交于![]() 、
、![]() 两点(
两点(![]() ,
, ![]() 不是长轴端点),且以
不是长轴端点),且以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 在
在![]() 轴正半轴上的顶点,求证:直线过定点,并求出该定点的坐标.
轴正半轴上的顶点,求证:直线过定点,并求出该定点的坐标.
【答案】(1) ![]() ;(2)答案见解析.
;(2)答案见解析.
【解析】试题分析:(1)利用点在椭圆上及相切关系布列方程组,即可解得椭圆![]() 的标准方程;
的标准方程;
(2)联立方程易得: ![]() ,
, ![]() ,以
,以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 在
在![]() 轴正半轴上的顶点,∴
轴正半轴上的顶点,∴![]() ,即
,即![]() 或
或![]() ,经检验得到结果.
,经检验得到结果.
试题解析:
法一(Ⅰ)由题意设椭圆的标准方程为![]() (
(![]() ,
, ![]() 且
且![]() )
)
∵![]() 在椭圆上,∴
在椭圆上,∴![]() ①
①
由 得
得![]()
∵椭圆![]() 与直线
与直线![]() 相切,∴
相切,∴![]() ,
,
即![]() ②
②
由①②知![]() ,
, ![]()
故所求椭圆方程为![]()
法二:设椭圆为![]() (
(![]() ,
, ![]() 且
且![]() )则它在点
)则它在点![]() 处的切线为
处的切线为 ,它与
,它与![]() 表示同一直线,∴
表示同一直线,∴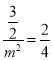 ,
, ![]() ,∴
,∴![]() ,
, ![]()
故所求椭圆方程为![]() .
.
(Ⅱ)设![]() ,
, ![]() ,联立
,联立
得![]()
![]() 得
得![]()
![]() ,
, ![]()
![]() ,
,
因为以![]() 为直径的圆过椭圆的上顶点
为直径的圆过椭圆的上顶点![]()
∴![]() 即
即![]()
∴![]()
即![]()
即![]()
即![]()
∴![]() 或
或![]()
当![]() 时,直线
时,直线![]() 过定点
过定点![]() 与已知矛盾
与已知矛盾
当![]() 时,直线
时,直线![]() 过定点
过定点![]() 满足
满足![]()
所以,直线![]() 过定点,定点坐标为
过定点,定点坐标为![]()


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】(2016·北京卷)如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=![]() .
.
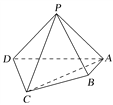
(1)求证:PD⊥平面PAB;
(2)求直线PB与平面PCD所成角的正弦值;
(3)在棱PA上是否存在点M,使得BM∥平面PCD?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0),四点P1(1,1),P2(0,1),P3(–1,
(a>b>0),四点P1(1,1),P2(0,1),P3(–1, ![]() ),P4(1,
),P4(1, ![]() )中恰有三点在椭圆C上.
)中恰有三点在椭圆C上.
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为–1,证明:l过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() .
.
(1)求圆心C的坐标及半径r的大小;
(2)已知不过原点的直线l与圆C相切,且在x轴、y轴上的截距相等,求直线l的方程;
(3)从圆外一点![]() 向圆引一条切线,切点为M,O为坐标原点,且
向圆引一条切线,切点为M,O为坐标原点,且![]() ,求点P的轨迹方程.
,求点P的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】庙会是我国古老的传统民俗文化活动,又称“庙市”或 “节场”.庙会大多在春节、元宵节等节日举行.庙会上有丰富多彩的文化娱乐活动,如“砸金蛋”(游玩者每次砸碎一颗金蛋,如果有奖品,则“中奖”).今年春节期间,某校甲、乙、丙、丁四位同学相约来到某庙会,每人均获得砸一颗金蛋的机会.游戏开始前,甲、乙、丙、丁四位同学对游戏中奖结果进行了预测,预测结果如下:
甲说:“我或乙能中奖”; 乙说:“丁能中奖”;
丙说:“我或乙能中奖”; 丁说:“甲不能中奖”.
游戏结束后,这四位同学中只有一位同学中奖,且只有一位同学的预测结果是正确的,则中奖的同学是( )

A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于![]() 若数列
若数列![]() 满足
满足![]() 则称这个数列为“
则称这个数列为“![]() 数列”.
数列”.
(Ⅰ)已知数列1, ![]() 是“
是“![]() 数列”,求实数
数列”,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)是否存在首项为![]() 的等差数列
的等差数列![]() 为“
为“![]() 数列”,且其前
数列”,且其前![]() 项和
项和![]() 使得
使得![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的通项公式;若不存在,请说明理由;
的通项公式;若不存在,请说明理由;
(Ⅲ)已知各项均为正整数的等比数列![]() 是“
是“![]() 数列”,数列
数列”,数列![]() 不是“
不是“![]() 数列”,若
数列”,若![]() 试判断数列
试判断数列![]() 是否为“
是否为“![]() 数列”,并说明理由.
数列”,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com