
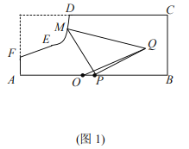
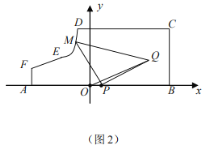
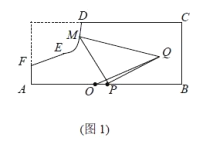
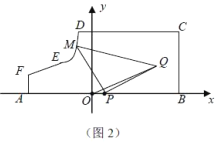
【题目】如图所示,某地区打算在一块矩形地块上修建一个牧场(ABCDEF围成的封闭区域)用来养殖牛和羊,其中AF=1,AB=10,BC=4,CD=7(单位:百米),DEF是一段曲线形马路.该牧场的核心区为等腰直角三角形MPQ所示区域,该区域用来养殖羊,其余区域养殖牛,且MP=PQ,牧场大门位于马路DEF上的M处,一个观察点P位于AB的中点处,为了能够更好观察动物的生活情况,现决定修建一条观察通道,起点位于距离观察点P处1百米的O点所示位置,终点位于Q处.如图2所示,建立平面直角坐标系,若![]() 满足
满足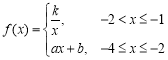 .
.
(1)求![]() 的解析式;
的解析式;
(2)求观察通道OQ长度的最小值.
【答案】(1)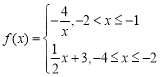 (2)
(2)![]() 百米
百米
【解析】
(1)依题意求出点![]() ,
,![]() ,
,![]() ,
,![]() 代入解析式即可求解;
代入解析式即可求解;
(2)过点M,Q分别作x轴的垂线,垂足为![]() ,
,![]() ,可得
,可得![]() ,
,
再对![]() 分类讨论,利用导数及二次函数的性质求出最小值;
分类讨论,利用导数及二次函数的性质求出最小值;
解:(1)因为AB=10,P是AB的中点,所以AP=5,
又OP=1,所以AO=4,所以![]() ,
,![]() ,
,
因为CD=7,BC=4,AF=1所以![]() ,
,![]()
由![]() 得,k=-4,所以
得,k=-4,所以![]() .
.
故![]() ,又
,又![]() ,所以
,所以![]() 解得
解得![]() ,
,
所以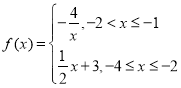
(2)过点M,Q分别作x轴的垂线,垂足为![]() ,
,![]() ,
,
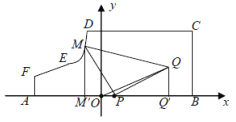
则![]() ,
,
又因为PM⊥PQ,所以![]()
所以![]() ,又因为PM=PQ,所以
,又因为PM=PQ,所以![]() ,
,
所以,由![]() ,可得
,可得![]() ,
,
①若![]() ,设
,设![]() ,则
,则![]() ,
,
![]() .
.
令![]() ,则
,则![]()
![]() ,因为
,因为![]() ,所以
,所以![]()
所以![]() 在
在![]() 上单调减,所以
上单调减,所以![]()
设![]() ,则
,则![]() 在
在![]() 上单调减
上单调减
所以![]() ,所以
,所以![]()
②若![]() ,设
,设![]() ,则
,则![]() ,
,
![]() ,
,
![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]() 时,
时,![]() ,
,
所以OQ的长度的最小值为![]() 百米.
百米.
答:观察通道OQ的长度的最小值为![]() 百米
百米


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 过点
过点![]()
(1)求抛物线![]() 的方程,并求其焦点坐标与准线方程;
的方程,并求其焦点坐标与准线方程;
(2)直线![]() 与抛物线
与抛物线![]() 交于不同的两点
交于不同的两点![]() ,
,![]() 过点
过点![]() 作
作![]() 轴的垂线分别与直线
轴的垂线分别与直线![]() ,
,![]() 交于
交于![]() ,
,![]() 两点,其中
两点,其中![]() 为坐标原点.若
为坐标原点.若![]() 为线段
为线段![]() 的中点,求证:直线
的中点,求证:直线![]() 恒过定点.
恒过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC-A1B1C1中,AA1![]() AB
AB![]() AC
AC![]() 2,AB⊥AC,M是棱BC的中点点P在线段A1B上.
2,AB⊥AC,M是棱BC的中点点P在线段A1B上.
(1)若P是线段A1B的中点,求直线MP与直线AC所成角的大小;
(2)若![]() 是
是![]() 的中点,直线
的中点,直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求线段BP的长度.
,求线段BP的长度.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数y=f1(x)的图象以原点为顶点且过点(1,1),反比例函数y=f2(x)的图象与直线y=x的两个交点间距离为8,f(x)= f1(x)+ f2(x).
(Ⅰ) 求函数f(x)的表达式;
(Ⅱ) 证明:当a>3时,关于x的方程f(x)= f(a)有三个实数解.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=3,直线PA与圆O相切于点A,直线PB垂直y轴于点B,且|PB|=2|PA|.
(1)求点P的轨迹E的方程;
(2)过点(1,0)且与x轴不重合的直线与轨迹E相交于P,Q两点,在x轴上是否存在定点D,使得x轴是∠PDQ的角平分线,若存在,求出D点坐标,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直四棱柱![]() 中,底面
中,底面![]() 是边长为6的正方形,点
是边长为6的正方形,点![]() 在线段
在线段![]() 上,且满足
上,且满足![]() ,过点
,过点![]() 作直四棱柱
作直四棱柱![]() 外接球的截面,所得的截面面积的最大值与最小值之差为
外接球的截面,所得的截面面积的最大值与最小值之差为![]() ,则直四棱柱
,则直四棱柱![]() 外接球的半径为( )
外接球的半径为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
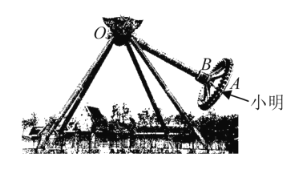
【题目】如图,大摆锤是一种大型游乐设备,常见于各大游乐园.游客坐在圆形的座舱中,面向外.通常大摆锤以压肩作为安全束缚,配以安全带作为二次保险.座舱旋转的同时,悬挂座舱的主轴在电机的驱动下做单摆运动.今年五一,小明去某游乐园玩“大摆锤”,他坐在点A处,“大摆锤”启动后,主轴![]() 在平面
在平面![]() 内绕点O左右摆动,平面
内绕点O左右摆动,平面![]() 与水平地面垂直,
与水平地面垂直,![]() 摆动的过程中,点A在平面
摆动的过程中,点A在平面![]() 内绕点B作圆周运动,并且始终保持
内绕点B作圆周运动,并且始终保持![]() ,
,![]() .已知
.已知![]() ,在“大摆锤”启动后,给出下列结论:
,在“大摆锤”启动后,给出下列结论:
①点A在某个定球面上运动;
②线段![]() 在水平地面上的正投影的长度为定值;
在水平地面上的正投影的长度为定值;
③直线![]() 与平面
与平面![]() 所成角的正弦值的最大值为
所成角的正弦值的最大值为![]() ;
;
④![]() 与水平地面所成角记为
与水平地面所成角记为![]() ,直线
,直线![]() 与水平地面所成角记为
与水平地面所成角记为![]() ,当
,当![]() 时,
时,![]() 为定值.
为定值.
其中正确结论的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com