
(Ⅱ)已知函数y=![]() 在(0,+∞)上单调递增,求证:当xl、x2>0时,f(x1)+f(x2)<f(x1+x2);
在(0,+∞)上单调递增,求证:当xl、x2>0时,f(x1)+f(x2)<f(x1+x2);
(Ⅲ)求证:![]() (n≥2,n∈N*).
(n≥2,n∈N*).
答案:证明:(Ⅰ)要证ln![]() ,只证ln(1+
,只证ln(1+![]() )<
)<![]() .
. ![]()
令t=![]() ,只证ln(1+t)<t.
,只证ln(1+t)<t.
令g(t)=ln(1+t)-t(t>-1,且t≠0,此时x>0或x<-1).
则g′(t)=![]() .
.
当-1<t<0时,g′(t)>0;当t>0时,g′(t)<0.∴当t>-1时,g(t)≤g(0),即ln(1+t)-t≤0.∵t≥-1且t≠0,∴ln(1+t)<t.∴ln![]() 成立.
成立.
(Ⅱ)由x1>0,x2>0,有x1+x2>x1,x1+x2>x2.∵![]() 在(0,+∞)上单调递增,
在(0,+∞)上单调递增,
∴![]()
∴f(x1)<![]() f(x1+x2),f(x2)<
f(x1+x2),f(x2)<![]() f(x1+x2).
f(x1+x2).
∴f(x1)+f(x2)<f<x1+x2).
(Ⅲ)由(Ⅱ)推广,有f(x1)+f<x2)+…+f<xn)<f(x1+x2+…+xn).
要证![]() ln2+
ln2+![]() ln3+…+
ln3+…+![]() lnn>
lnn>![]() ,
,
只证![]() ln22+
ln22+![]() ln32+…+
ln32+…+![]() lnn2>
lnn2>![]() .
.
即证![]() ln
ln![]() +
+![]() ln
ln![]() +…+
+…+![]() ln
ln![]() <
<![]()
令f(x)=xlnx(x>o),则![]() =lnx在(0,+∞)上单调递增.
=lnx在(0,+∞)上单调递增.
要证原不等式成立,只证
![]()
又![]()
![]() .
.
由![]() =
=![]() (其中k=l,2,…,n-1).
(其中k=l,2,…,n-1).
∴![]() .
.
∴1n(![]() )<ln(l
)<ln(l![]() ),
),
又由(Ⅰ),ln(1![]() )<
)<![]() (n≥2),∴ln(
(n≥2),∴ln(![]() )<
)<![]() <0,
<0,
且![]() >
>![]()
∴(![]() )ln(
)ln(![]() )<
)<![]() .
.
∴![]() .
.
∴原不等式成立.
(Ⅲ)另证:∵![]() ln2+
ln2+![]() ln3+…+
ln3+…+![]() lnn>
lnn>![]() ln2.
ln2.
而![]() ln2>
ln2>![]()
![]() ln2>
ln2>![]()
![]() 3ln2>1
3ln2>1![]() 1n8>1
1n8>1![]() 8>e,
8>e,
又![]()
![]() <3n-3<n2+n
<3n-3<n2+n![]() n2-2n+3>0
n2-2n+3>0![]() (n-1)2+2>0.
(n-1)2+2>0.
∴![]() .∴结论成立.
.∴结论成立.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源:成都二模 题型:单选题
| A.{x|x≥2} | B.{x|x>2} | C.{x|x≤0或x≥2} | D.{x|0<x<2} |
查看答案和解析>>
科目:高中数学 来源:广东省高考数学一轮复习:2.2 一元二次不等式(1)(解析版) 题型:选择题
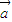 =(x,-1)与
=(x,-1)与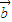 =(1,
=(1,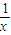 ),则不等式
),则不等式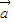 •
• ≤0的解集为( )
≤0的解集为( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com