
【题目】甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在7,8,9,10环,且每次射击成绩互不影响.射击环数的频率分布条形图如下:

若将频率视为概率,回答下列问题:
(1)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率;
(2)若甲、乙两运动员各自射击1次,![]() 表示这2次射击中击中9环以上(含9环)的次数,求
表示这2次射击中击中9环以上(含9环)的次数,求![]() 的分布列及期望
的分布列及期望![]() .
.
【答案】(1)0.992;(2)见解析
【解析】
((1)设甲运动员在3次射击中至少有1次击中9环以上(含9环)为事件![]() ,结合
,结合![]() 次独立重复试验中恰好发生
次独立重复试验中恰好发生![]() 次的概率公式即可求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率.
次的概率公式即可求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率.
(2)根据题意,![]() 表示这2次射击中击中9环以上(含9环)的次数的取值是0、1、2,根据互斥事件和相互独立事件同时发生的概率做出结果分布列和期望.
表示这2次射击中击中9环以上(含9环)的次数的取值是0、1、2,根据互斥事件和相互独立事件同时发生的概率做出结果分布列和期望.
(1)设事件![]() 表示“甲运动员射击一次,恰好命中
表示“甲运动员射击一次,恰好命中![]() 环以上(含
环以上(含![]() 环,下同)”,
环,下同)”,
则![]() .
.
甲运动员射击![]() 次,均未击中
次,均未击中![]() 环以上的概率为
环以上的概率为
![]() .
.
所以甲运动员射击![]() 次,至少
次,至少![]() 次击中
次击中![]() 环以上的概率
环以上的概率
![]() .
.
(2)记事件![]() 表示“乙运动员射击一次,击中
表示“乙运动员射击一次,击中![]() 环以上”,
环以上”,
则![]() .
.
因为![]() 表示2次射击击中9环以上的次数,所以
表示2次射击击中9环以上的次数,所以![]() 的可能取值是0,1,2.
的可能取值是0,1,2.
因为![]()
![]()
![]()
所以![]() 的分布列是
的分布列是
X | 0 | 1 | 2 |
P | 0.05 | 0.35 | 0.6 |
所以![]()


科目:高中数学 来源: 题型:
【题目】抛物线C:y2=4x的焦点为F,斜率为k的直线l与抛物线C交于M,N两点,若线段MN的垂直平分线与x轴交点的横坐标为a(a>0),n=|MF|+|NF|,则2a﹣n等于( )
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C所对的边分别为a,b,c,已知向量 ![]() =(2a,1),
=(2a,1), ![]() =(2b﹣c,cosC),且
=(2b﹣c,cosC),且 ![]() ∥
∥ ![]() .
.
(Ⅰ)求角A的大小;
(Ⅱ)若 ![]() ,求b+c的取值范围.
,求b+c的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx﹣a(x﹣1),其中a为实数.
(Ⅰ)讨论并求出f(x)的极值;
(Ⅱ)在a<1时,是否存在m>1,使得对任意的x∈(1,m)恒有f(x)>0,并说明理由;
(Ⅲ) 确定a的可能取值,使得存在n>1,对任意的x∈(1,n),恒有|f(x)|<(x﹣1)2 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域为(0,+∞),f′(x)为f(x)的导函数,且满足xf′(x)>f(x),则不等式(x﹣1)f(x+1)>f(x2﹣1)的解集是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某地有三家工厂,分别位于矩形ABCD的顶点A,B以及CD的中点P处,已知AB=20km,CB=10km,为了处理三家工厂的污水,现要在矩形ABCD内(含边界),且与A,B等距离的一点O处建造一个污水处理厂,并铺设排污管道AO,BO,OP,设排污管道的总长为![]() km.
km.
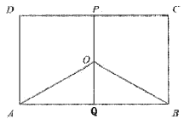
(I)设![]() ,将
,将![]() 表示成
表示成![]() 的函数关系式;
的函数关系式;
(II)确定污水处理厂的位置,使三条排污管道的总长度最短,并求出最短值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了探究车流量与![]() 的浓度是否相关,现采集到华中某城市2015年12月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到华中某城市2015年12月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)求![]() 关于
关于![]() 的线性回归方程;(提示数据:
的线性回归方程;(提示数据: ![]() )
)
(2)(I)利用(1)所求的回归方程,预测该市车流量为12万辆时![]() 的浓度;(II)规定:当一天内
的浓度;(II)规定:当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为优;当一天内
内,空气质量等级为优;当一天内![]() 的浓度平均值在
的浓度平均值在![]() 内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量不超过多少万辆?(结果以万辆为单位,保留整数)参考公式:回归直线的方程是
内,空气质量等级为良,为使该市某日空气质量为优或者为良,则应控制当天车流量不超过多少万辆?(结果以万辆为单位,保留整数)参考公式:回归直线的方程是![]() ,其中
,其中 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com