
【题目】在![]() 中,内角
中,内角![]() ,
,![]() ,
,![]() 的对边分别是
的对边分别是![]() ,
,![]() ,
,![]() ,且满足:
,且满足:![]() .
.
(Ⅰ)求角![]() 的大小;
的大小;
(Ⅱ)若![]() ,求
,求![]() 的最大值.
的最大值.
科目:高中数学 来源: 题型:
【题目】2019年10月17日是全国第五个“扶贫日”,在“扶贫日”到来之际,某地开展“精准扶贫,携手同行”的主题活动,调查基层干部走访贫困户数量.A镇有基层干部50人,B镇有基层干部80人,C镇有基层干部70人,每人都走访了不少贫困户;按照分层抽样,从A,B,C三镇共选40名基层干部,统计他们走访贫困户的数量,并将完成走访数量分成5组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,绘制成如下频率分布直方图.
,绘制成如下频率分布直方图.
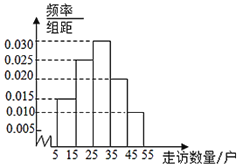
(1)求这40人中有多少人来自B镇,并估算这40人平均走访多少贫困户?
(2)如果把走访贫困户达到或超过25户视为工作出色,以频率估计概率,从三镇的所有基层干部中随机选取4人,记这4人中工作出色的人数为X,求X的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 为椭圆E:
为椭圆E:![]() 的左、右焦点,过点
的左、右焦点,过点![]() 的直线l与椭圆E有且只有一个交点T.
的直线l与椭圆E有且只有一个交点T.
(1)求![]() 面积的取值范围.
面积的取值范围.
(2)若有一束光线从点![]() 射出,射在直线l上的T点上,经过直线l反射后,试问反射光线是否恒过定点?若是,请求出该定点;若否,请说明理由.
射出,射在直线l上的T点上,经过直线l反射后,试问反射光线是否恒过定点?若是,请求出该定点;若否,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某中学学生对《中华人民共和国交通安全法》的了解情况,调查部门在该校进行了一次问卷调查(共12道题),从该校学生中随机抽取40人,统计了每人答对的题数,将统计结果分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 六组,得到如下频率分布直方图.
六组,得到如下频率分布直方图.
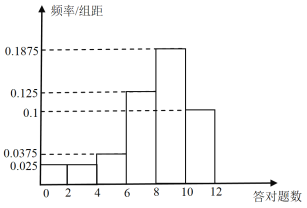
(1)若答对一题得10分,未答对不得分,估计这40人的成绩的平均分(同一组中的数据用该组区间的中点值作代表);
(2)若从答对题数在![]() 内的学生中随机抽取2人,求恰有1人答对题数在
内的学生中随机抽取2人,求恰有1人答对题数在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x)满足f(e+x)=f(e﹣x),且f(0)=0,当x∈(0,e]时,f(x)=lnx已知方程![]() 在区间[﹣e,3e]上所有的实数根之和为3ea,将函数
在区间[﹣e,3e]上所有的实数根之和为3ea,将函数![]() 的图象向右平移a个单位长度,得到函数h(x)的图象,,则h(7)=_____.
的图象向右平移a个单位长度,得到函数h(x)的图象,,则h(7)=_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高考的成绩不仅需要平时的积累,还与考试时的状态有关系.为了了解考前学生的紧张程度与性别是否有关系,现随机抽取某校500名学生进行了调查,结果如表所示:
心情 性别 | 男 | 女 | 总计 |
正常 | 30 | 40 | 70 |
焦虑 | 270 | 160 | 430 |
总计 | 300 | 200 | 500 |
(1)根据该校调查数据,能否在犯错误的概率不超过0.01的前提下,认为“该学校学生的考前焦虑情况与性别有关”?
(2)若从考前心情正常的学生中按性别用分层抽样的方法抽取7人,再从被抽取的7人中随机抽取2人,求这两人中有女生的概率.
附: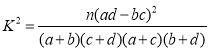 ,
,![]() .
.
| 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
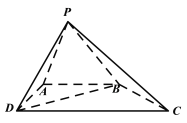
(1)求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在点
上是否存在点![]() ,使得平面
,使得平面![]() 与平面
与平面![]() 所成锐二面角为
所成锐二面角为![]() ?若存在,求
?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com